Такие сумматоры имеют максимальное быстродействие. В них отсутствует распространение переноса от разряда к разряду. В каждом разряде одновременно вырабатываются выходные величины.
Возможность построения сумматора с такими свойствами основана на воспроизведении функций суммы и переноса, зависящих только от значений слагаемых независимо от местоположения разряда в разрядной сетке.
В первом – младшем разряде реализуются функции, зависящие только лишь от слагаемых данного разряда:
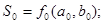
Во втором разряде реализуются функции.
которые зависят как от слагаемых данного разряда, так и от переноса из первого разряда. Однако этот перенос является функцией слагаемых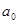 
и 
, поэтому 
и 
можно выразить:
Аналогично для разряда с индексом 
:
В последнем (старшем) разряде:
По приведенным выражениям можно получать значения разрядных сумм во всех разрядах одновременно, так как все аргументы искомых функций появляются сразу при поступлении слагаемых на входы сумматора.
Для сокращения записи введем функции генерации и передачи переноса.
Структура формулы, определяющей функцию переноса:
.
Первое слагаемое равно единице, когда перенос из данного разряда порождается (генерируется) независимо от значения переноса из предыдущих в данный. Поэтому функция генерации переноса:
.
Выражение в скобках, являющееся множителем для значения переноса из предыдущего разряда, определяет условия, при которых перенос на выходе возникает как следствие поступления в данный разряд входного переноса. Иначе: при единичном значении выражения в скобках разряд функционирует как передатчик переноса. Определим функцию передачи переноса:
.
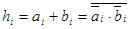Теперь перенос из данного разряда выражается:
.
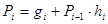В соответствии с этой формулой:
(
- внешний перенос).
Выражаем перенос через функцию И-НЕ.
Полученным выражениям соответствует схема параллельного сумматора с параллельным переносом, представляющая совокупность не связанных между собой какими-либо цепями передачи переноса разрядных схем:
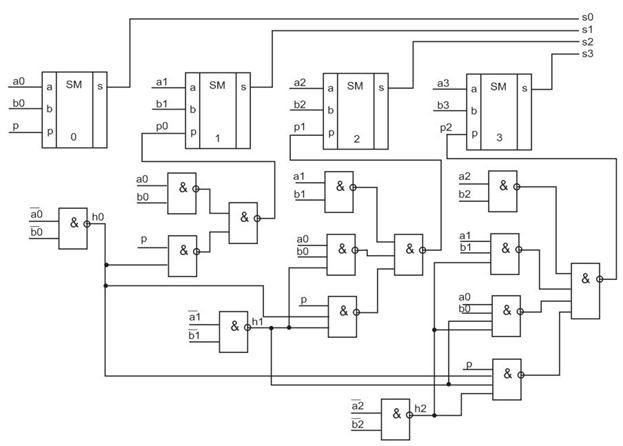
Длительность суммирования при параллельном переносе не зависит от разрядностей слагаемых (если пренебречь зависимостью задержек элементов от нагрузки, возрастающей с ростом разрядности).
Для рассмотренного сумматора длительность суммирования складывается из задержек выработки функций передачи переноса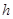 
- 
, времени формирования функций переноса - 2 и задержки одноразрядных сумматоров 
, то есть
Для сумматоров с параллельным переносом можно использовать упрощенные одноразрядные сумматоры, имеющие лишь один выход суммы.
В зависимости от типа одноразрядного сумматора время суммирования при параллельном переносе.
С ростом числа разрядов реализации параллельного переноса затрудняется, так как возникает потребность в элементах с большим числом входов и большой нагрузочной способностью. Уже при построении восьмиразрядного сумматора потребуются элементы с числом входов 8 и коэффициентом разветвления 16. Обычно реализуют сумматоры с параллельным переносом лишь для малого числа разрядов как составные части сумматоров с групповой структурой.
Сумматоры с групповой структурой, имеющие n разрядов, состоят из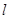 
групп по m разрядов. В группах и между ними возможны различные виды переносов.
Сумматор с цепным переносом снабжен блоками переносов БП анализирующими слагаемыми в пределах группы:
Ясно, что при этом меньше размерность схем, вырабатывающих переносы, так как не требуется учета всех предыдущих разрядов для сумматоров в целом. Одновременно с этим появляется последовательная передача переноса между группами.
Перенос из группы определяется через функции генерации и передачи переносов разрядов следующим образом:
(
), 
- входной перенос группы.
Блок переносов для 
имеет вид:
Длительность суммирования оценивается:
- время задержки выработки функции передачи переноса в группе;
- время задержки в блоке переноса;
- время суммирования в группе.
Для 32-х разрядного сумматора из 8 групп с параллельным переносом в группах длительность суммирования» 20¸25 задержек логических элементов.
Сумматор с параллельно-параллельным переносом имеет параллельный перенос как в группах, так и между ними, это обеспечивает минимальное время суммирования.
В таком сумматоре дважды (в группах и между ними) повторяется принципиально идентичная организация переносов, причем для сумматоров в целом группы играют ту же роль, что и одноразрядные сумматоры для группы.
Для групп вырабатываются функции генерации и передачи переносов, причем функции генерации:
Эта функция принимает единичное значение, если из данной группы появляется перенос не зависимо от наличия или отсутствия входного переноса.
Функция передачи переносов:
принимает единичное значение, если выходной перенос из группы появляется только при наличии входного.
Заметим, что функции передачи переносов 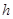и 
называют функциями прозрачности или транзита.
В данном случае термин «функция прозрачности» хорошо поясняет соотношение для : группа прозрачна при прозрачности всех ее разрядов.
Сигнал переноса для группы вырабатывается согласно выражению:
Сумматор с четырьмя 4-х разрядными группами имеет вид:
С помощью групп вырабатываются значения суммы в пределах группы, складывая поля слов 
и 
так далее.
Сигналы переносов для групп формируются с помощью блоков 
, и , реализующих записанные выше выражения.
Анализируя работу – вывод 
.
Если число разрядов велико – те же трудности, что в простом параллеьном сумматоре.
Распространяют способ организации на схему с тремя уровнями. Рассмотрим групповой – часть схемы. Между частями вновь организуется параллельный перенос (как бы трехкратное вложение сумматора с параллельным переносом).
