Решение. Будем считать, что распределение частоты у исправного и неисправного преобразователей подчиняется нормальному закону

Будем считать, что распределение частоты у исправного и неисправного преобразователей подчиняется нормальному закону, а С ₁₁ = С ₂₂ = 0. Тогда из условия (6.30) получим

где Р ₂ = 0,05 и P ₁ = 1- Р ₂ = 0,95 - вероятности пребывания преобразователя частоты соответственно в неисправном и исправном состояниях. Плотности распределения при нормальном законе

;

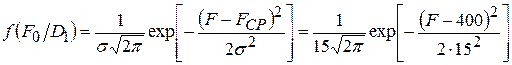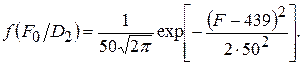
Подставим полученные значения в предыдущее равенство и, логарифмируя его, получим

-(F - 400)² / (2×15²) + (F - 430)² / (2×50²) = ln(2,632× 15 / 50) = - 0,2362.

Это уравнение можно упростить:

F ² - 0,794×10³× F + 15,74×10⁴ = 0.

Положительный корень этого уравне­ния F ₀ = 411,46. Следовательно, мож­но рассчитывать на то, что до часто­ты 411,46 Гц преобразователь будет работать нормально. Очевидно, что отклонение частоты преобразователя от его среднего значения не должно превышать 411,46 – 400 = 11,46 Гц при его нормальной работе. Полученное решение может быть проиллюстрировано графиче­ски на рисунке 6.3, если принять х ₁ = 400 Гц, х ₂ = 430 Гц, а х ₀ = 411,46 Гц.

Метод наибольшего правдоподобия, как и метод минимального рис­ка, для записи своего решающего правила использует отношение правдоподобия

x Î D ₁, если f (х / D ₁) / f (х/D ₂) > 1; (6.37)

x Î D ₂,если f(х/D1) / f (х/D ₂) < 1, (6.38)

где x - диагностируемый параметр.

Граничное значение х = х ₀ находят из следую­щего условия:

f (х/D ₁) = f (х/D ₂). (6.39)

Сравнивая (6.39), (6.35) и (6.30), видим, что они совпадают, если

λ = P ₂×(С ₁₂ - С ₂₂) / [ P ₁×(С ₂₁ - С ₁₁)] = 1. (6.40)

Из этого следует, что метод наибольшего правдоподо­бия является частным случаем метода минимального риска. При С ₁₁ = С ₂₂ = 0 (6.40) приобретает вид

P ₂ С ₁₂ / (P ₁ С ₂₁) = 1. (6.41)

Отметим в заключение, что всегда надо иметь в виду, что P ₁ >> Ρ ₂ и С ₁₂ >> С ₂₁. Метод наибольшего правдоподобия проиллюстрируем примером 6.8.

Пример 6.8 [1].

Условия задачи совпадают с примером 6.7. Необходимо решить ее методом наибольшего правдоподобия.