I:{{1026}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения 
по виду его правой части соответствует функция ###
-: 
-: 
+: 
-: 
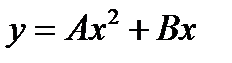
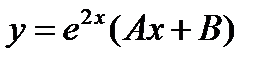
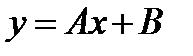
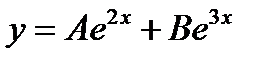
I:{{1027}} Э,С; t=0; k=4; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения 
по виду его правой части соответствует функция ###
-: 
+: 
-: 
-: 
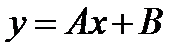
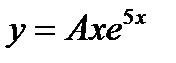
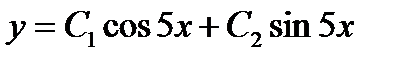
I:{{1028}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения 
по виду его правой части соответствует функция ###
+: 
-: 
-: 
-: 
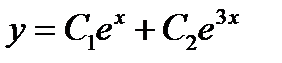
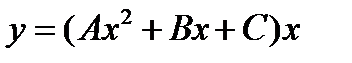
I:{{1029}} Э,С; t=0; k=4; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения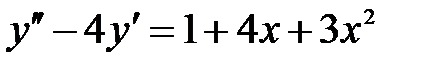 
по виду его правой части соответствует функция ###
-: 
-: 
-:
+:
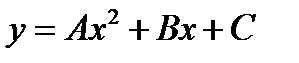
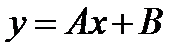
I:{{1030}} Э,С; t=0; k=4; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения 
по виду его правой части соответствует функция ###
-:
-:
-:
+:
I:{{1031}} Э,С; t=0; k=4; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения 
по виду его правой части соответствует функция ###
-:
+:
-:
-:
I:{{1032}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения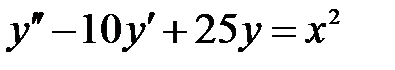 
по виду его правой части соответствует функция ###
+:
-:
-:
-:
I:{{1033}} Э,С; t=0; k=4; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения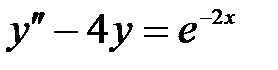 
по виду его правой части соответствует функция ###
-:
-:
+:
-:
I:{{1034}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения 
по виду его правой части соответствует функция ###
-:
-:
+:
-:
I:{{1035}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Частному решению линейного неоднородного дифференциального уравнения 
по виду его правой части соответствует функция ###
-:
+:
-:
-: