I:{{996}} С; t=0; k=4; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями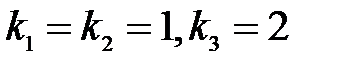 
является ###
-: 
-: 
-: 
+: 
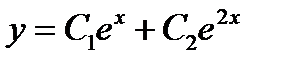
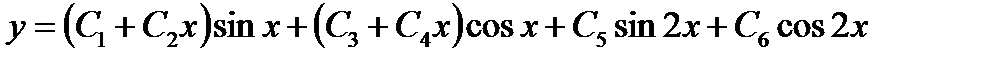
I:{{997}} С; t=0; k=4; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
+: 
-: 
-: 
-: 
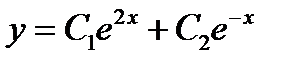
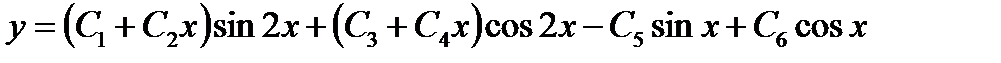
I:{{998}} С; t=0; k=4; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
-: 
+: 
-: 
-: 
I:{{999}} С; t=0; k=4; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
+: 
-: 
-: 
-: 
I:{{1000}} С; t=0; k=4; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
-: 
+: 
-: 
-: 
I:{{1001}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
-: 
+: 
-: 
-: 
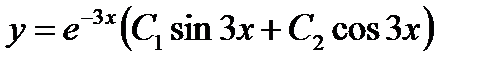
I:{{1002}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями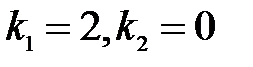 
является ###
-: 
-: 
+: 
-: 
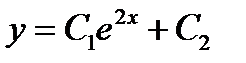
I:{{1003}} Э.С; t=0; k=3; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
-: 
-: 
+: 
-: 
I:{{1004}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
-: 
-: 
+: 
-: 
I:{{1005}} Э,С; t=0; k=3; ek=0; m=0; c=0;
S: Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 
является ###
-: 
-: 
-: 
+: 
