Если на вход устойчивого линейного звена с передаточной функцией  подается гармонический сигнал
подается гармонический сигнал 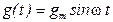 , где
, где 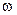 — угловая частота, а
— угловая частота, а 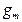 — амплитуда, то на его выходе в установившемся режиме будет гармонический сигнал
— амплитуда, то на его выходе в установившемся режиме будет гармонический сигнал  той же частоты
той же частоты 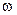 , но, в общем случае, с другой амплитудой
, но, в общем случае, с другой амплитудой  и ненулевым фазовым сдвигом
и ненулевым фазовым сдвигом  (см рис.5.1, где
(см рис.5.1, где 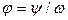 — временной интервал, соответствующий фазовому сдвигу
— временной интервал, соответствующий фазовому сдвигу  ).
).
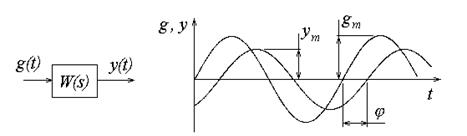
Рис. 5.1. Реакция устойчивого линейного звена на гармонический сигнал
Для аналитического описания частотных свойств динамических звеньев используется частотная передаточная функция 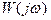 , которая для фиксированной частоты
, которая для фиксированной частоты 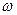 представляет собой комплексное число, модуль которого равен отношению амплитуды выходного сигнала к амплитуде входного сигнала, а аргумент — сдвигу фаз между входным и выходным сигналами.В более общей формулировке частотная передаточная функция определяется как отношение изображений Фурье выходного и входного сигналов. Формальное правило получения аналитического выражения для частотной передаточной функции по известной передаточной функции
представляет собой комплексное число, модуль которого равен отношению амплитуды выходного сигнала к амплитуде входного сигнала, а аргумент — сдвигу фаз между входным и выходным сигналами.В более общей формулировке частотная передаточная функция определяется как отношение изображений Фурье выходного и входного сигналов. Формальное правило получения аналитического выражения для частотной передаточной функции по известной передаточной функции  состоит в подстановке
состоит в подстановке 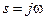 , т.е.
, т.е.  , что соответствует переходу от изображения Лапласа к изображению Фурье.
, что соответствует переходу от изображения Лапласа к изображению Фурье.
Частотная передаточная функция (ЧПФ) может быть представлена в виде:
 или
или 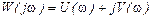 ,
,
где  — вещественная часть,
— вещественная часть,  — мнимая часть,
— мнимая часть, 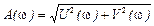 — модуль, а
— модуль, а  — аргумент (фаза) ЧПФ.
— аргумент (фаза) ЧПФ.
С помощью частотной передаточной функции могут быть построены следующие частотные характеристики.
Амплитудно-частотная характеристика (АЧХ) — зависимость 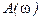 при изменениичастоты
при изменениичастоты 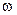 от
от 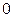 до
до  (рис. 5.2).
(рис. 5.2).
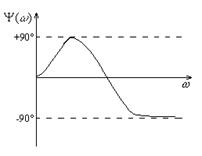
Фазовая частотная характеристика (ФЧХ) — зависимость  при изменении частоты
при изменении частоты 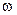 от
от 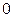 до
до  (рис. 5.3).
(рис. 5.3).

| 
|
| Рис. 5.2. Амплитудно-частотная характеристика | Рис. 5.3. Фазовая частотная характеристика |
| 
|
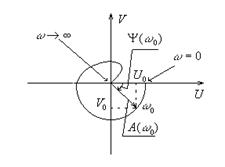
| Рис. 5.4. Амплитудно-фазовая частотная характеристика | Рис. 5.5. Логарифмические амплитудная и фазовая частотные характеристики |
Амплитудно-фазовая частотная характеристика (АФЧХ) — годограф, соответствующий частотной передаточной функции при изменении частоты от 0 до  , построенный на комплексной плоскости
, построенный на комплексной плоскости 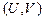 (рис.5.4). При этом за положительное значение фазы понимается направление вращения от вещественной оси против часовой стрелки.
(рис.5.4). При этом за положительное значение фазы понимается направление вращения от вещественной оси против часовой стрелки.
Логарифмические амплитудная и фазовая частотные характеристики (ЛАЧХ и ЛФЧХ). При построении логарифмической амплитудной частотной характеристики по оси ординат откладывается величина 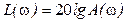 , единицей измерения которой является децибел (дБ). По оси абсцисс откладывается частота
, единицей измерения которой является децибел (дБ). По оси абсцисс откладывается частота 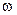 в логарифмическом масштабе (рис. 5.5). Ось ординат может пересекать ось абсцисс в произвольном месте. Поэтому ее проводят так, чтобы справа от нее отобразить интересующий диапазон частот. Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза
в логарифмическом масштабе (рис. 5.5). Ось ординат может пересекать ось абсцисс в произвольном месте. Поэтому ее проводят так, чтобы справа от нее отобразить интересующий диапазон частот. Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза 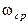 . В инженерных расчетах используют асимптотические ЛАХ, которые можно построить практически без вычислительной работы. Подобные характеристики представляют собой ломанную линию, состоящую из отрезков, расположенных к оси абсцисс под углами, кратными
. В инженерных расчетах используют асимптотические ЛАХ, которые можно построить практически без вычислительной работы. Подобные характеристики представляют собой ломанную линию, состоящую из отрезков, расположенных к оси абсцисс под углами, кратными 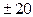 дБ/дек. Логарифмическая фазовая частотная характеристика отличается от ФЧХ только тем, что ось абсцисс строится в логарифмическом масштабе.
дБ/дек. Логарифмическая фазовая частотная характеристика отличается от ФЧХ только тем, что ось абсцисс строится в логарифмическом масштабе.






