Типовыми динамическими звеньями называются простейшие составные части системы, поведение которых описывается обыкновенными дифференциальными уравнениями 0-2-го порядка:
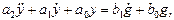(2.1)
где 
- входная переменная звена,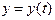 
-выходная переменная; 
-постоянные коэффициенты (параметры).
Переходным процессом называется изменение во времени переменных (сигналов) динамической системы или звена: 
, 
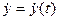, обусловленное начальными условиями или входным воздействием.
| Переходной функцией системы или звена y = h (t)называется переходный процесс выходной переменной при единичном входном воздействии g =1(t) (рис.2.1) и нулевых начальных условиях.. | 
Рис.2.1
|
По графику переходной функции может быть определена математическая модель исследуемого динамического звена и ее параметры
Передаточные функции типовых динамических звеньев в общем случае являются произведением сомножителей:
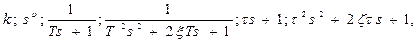
где k, τ, T, υ, ξ - постоянные, причем k >0; υ может быть положительным и отрицательным целым числом; T>0; 0£τ<1; 0£ξ<1.
Перечисленные сомножители определяют различные типы динамических звеньев, среди которых выделяется подкласс позиционных, представленный в таблице 2.1. (p - оператор дифференцирования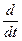 
, s - комплексная величина).
Позиционные звенья, кроме консервативного, характеризуются тем, что в каждом из них при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины. Отношение установившихся значений выходной и входной величин есть передаточный коэффициент k звена.
В безынерционном (идеальном) звене при скачкообразном изменении входной величины мгновенно изменяется и выходная величина, т. е. переходного процесса нет. В апериодическом (инерционном) звене выходная величина нарастает монотонно, т. е. имеет место переходной процесс. Его продолжительность зависит от постоянной времени Т, являющейся параметром звена.
В апериодическом звене второго порядка продолжительность переходного процесса зависит от двух постоянных: Т 1 и Т 2.
Таблица 2.1
| Тип звена | Дифференциальное уравнение в операторном виде | Передаточная функция W=W(s) |
| Идеальное усилительное (безынерционное) | y=kx | W=k |
| Апериодическое (инерционное) | (Tp+1)y=kx | k W = ---------- Ts+1 |
 Апериодическое (инерционное) второго порядка
| (T22p2+T1p+1)y=kx; где T1 ³ 2T2 | k k W =----------------= -------------------, T22s2+T1s+1 (T3s+1)(T4s+1) где T3,4= 0.5 ´ (T1 ±Ö T12-4T22) |
| Колебательное | (T2p2+2xTp+1)y=kx, где 0< x <1 | k W = ----------------- T2s2+2xTs+1 |
| Консервативное | (T2p2+1)y=kx; | k W = ---------- T2s2+1 |
Апериодическое звено второго порядка также можно представить как последовательное соединение двух апериодических звеньев первого порядка.
Выходная величина колебательного звена в переходном процессе колеблется около того значения, которое должно установится. Затухание колебаний зависит от коэффициента демпфирования x. Точнее, скорость затухания характеризуется коэффициентом затухания a=x/T.
Угловая частота колебаний b = Ö1-x2/Т.
Консервативное звено есть частный случай колебательного звена (x=0) и характеризуется незатухающими колебаниями при постоянном воздействии на входе.
Во временной области переходные характеристики описываются выражениями, представленными в таблице 2.2.
Таблица 2.2
| N | Тип звена | Переходная характеристика h = h(t) |
| Идеальное усилительное (безынерционное) | h = k | |
| Апериодическое (инерционное) |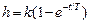 
| |
| Апериодическое (инерционное) второго порядка |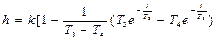 
| |
| Колебательное |  .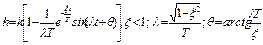
| |
| Консервативное | 
|
Амплитуда первого положительного выброса переходного процесса в колебательном звене определяется выражением
. (2.1)
А амплитуда первого отрицательного s2 выброса связана с s1 отношением
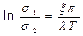. (2.2)
При ξ > 1трение в системе, рассеивание энергии, относительно велико и колебательность переходной функции исчезает, функция становится монотонной.
Постоянная времени Т колебательного звена не равна периоду колебаний Ткол, она связана с периодом, но существенно меньше его: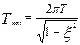 
при ξ < 0.5 период затухающих колебаний примерно равен Ткол ≈ 2 π Т.
По колебательной переходной характеристике звена можно приближенно оценить его параметры (рис 2.2):
- уровень успокоения колебаний равен коэффициенту усиления k звена;
- постоянная времени приближенно равна Т ≈ Ткол / 2π
- декремент затухания ξ ≈ 3Т / Тпер, где Тпер - длительность переходного процесса, определяемая промежутком времени, за которое переходная функция попадает в пятипроцентный коридор.
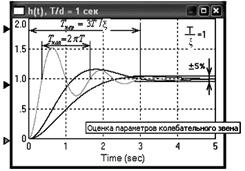
Рис. 2.2. Переходные характеристики колебательного звена
