Рис.2. Окончание
Ширина p-n перехода может быть найдена при интегрировании уравнения Пуассона, которое определяет распределение напряженности электрического поля E(x) и потенциала j(x). При этом получают:
,
где e - диэлектрическая проницаемость полупроводника; eо – диэлек-трическая проницаемость вакуума (диэлектрическая постоянная); e – заряд электрона; jК - контактная разность потенциалов; Nа - концентрация акцепторов; NД - концентрация доноров.
Так как Nа>>NД, то lp<<ln, и приближенно можно записать
.
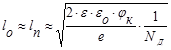Поскольку полупроводник в целом нейтрален, то объемные заряды в обеих частях p-n перехода равны (диаграмма 3 рис.2 отражает плоское сечение объемных зарядов), то есть Qp=e×Nа×lp×S, Qn=e×NД×ln×S, где S -
- площадь p-n перехода. Учитывая, что Qn=Qp или Nа×lp=NД×ln, получим соотношение Nа/NД=ln/lp - во сколько раз концентрация акцепторов больше концентрации доноров, во столько же раз ширина p-n перехода в полупроводнике n-типа больше ширины p-n перехода в полупроводнике
p-типа. В нашем случае Nа>>NД, а ln>>lp и p-n переход в основном находится в области полупроводника n-типа. Такие p-n переходы называются несимметричными переходами. Обычно ширина p-n перехода имеет значение: lо = (0,1¸1,0)мкм.
Распределение напряженности электрического поля и потенциала в p-n переходе (диаграммы 4 и 5 рис.2) получают из решения уравнения Пуассона:
,
где l(x) - плотность объемного заряда. Распределение плотности объемного заряда l(x) в p-n переходе аппроксимируют функцией l(x)=-e×Nа
при xÎ[0, lp].
Интегрируя данное уравнение Пуассона с учетом того, что на границах p-n перехода E=0, получают распределение напряженности электрического поля E(x), которое выражается кусочно-линейной функцией (диаграмма 4 рис.2), поскольку ее производная l(x) постоянна на участках
(-lp, 0) и (0, ln). Максимальная напряженность наблюдается на металлургической границе контакта двух полупроводников и приблизительно равна:
.
При увеличении концентрации примеси возрастает максимальное значение напряженности электрического поля в p-n переходе. Электрическое поле препятствует переходу основных носителей заряда через p-n переход. При контакте двух полупроводников возникает потенциальный барьер и распределение потенциала вдоль p-n перехода показано на диаграмме 5 рис.2. j(x) также получается путем двойного интегрирования уравнения Пуассона. Причем функция j(x) состоит из двух параболических участков, поскольку она получена интегрированием кусочно-линейной функции E(x) и имеет точку перегиба при x=0.
Высота потенциального барьера в равновесном состоянии равна контактной разности потенциалов jк.
,
где 
- потенциал работы выхода электрона дырочного полупроводника;
- потенциал работы выхода электрона электронного полупроводника. Для определения высоты потенциального барьера интегрирование E(x) проводится с учетом граничных условий: jр=0 при x=lp; jn=-jк при x=ln.
Поскольку значение jк отрицательно, то есть потенциальный барьер имеет отрицательную величину, то можно сделать вывод, что потенциальный барьер препятствует диффузии основных носителей заряда. Электрическое поле, возникающее в p-n переходе в процессе его образования, способствует переходу неосновных носителей заряда: электронов - в полупроводнике p-типа; дырок - в полупроводнике n-типа.
