Для сравнения двух нормально распределенных совокупностей, у которых есть различия в средних выборочных значениях, используют критерий Стьюдента. Фактический критерий рассчитывают по формуле:
где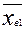 
- среднее значение первой выборочной совокупности;
- среднее значение второй выборочной совокупности;
- ошибка среднего для первой выборочной совокупности;
- ошибка среднего для второй выборочной совокупности.
Для вывода о достоверности различий между выборками используют ОСНОВНОЙ ПРИНЦИП проверки статистических гипотез. Нулевую гипотезу отвергают, если фактически установленная величина 
превзойдет или окажется равной критическому (стандартному) значению 
этой величины для принятого уровня значимости a и числа степеней свободы k=n1+n2-2 (если объемы выборок одинаковы).
П р и м е р: При изучении влияния некоторой пищевой добавки на прирост массы животных были получены следующие значения. В первой группе животных 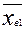=638 г, в контроле - =526 г. 
=402 и 
=382. Количество наблюдаемых животных в каждой группе было одинаковым: n1=n2 =9. Сделаем расчет: 
. В таблице критериев Стьюдента для k=n1+n2-2 =9±9-2=16 и уровня значимости a =0,05 находим =2,12. 
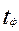> , следовательно верна альтернативная гипотеза (пищевая добавка влияет на прирост массы животных, или, другими словами, полученная в эксперименте разница в показаниях статистически достоверна).
