Математическая статистика - раздел прикладной математики, непосредственно примыкающий к теории вероятностей. Основное отличие математической статистики от теории вероятностей состоит в том, что в математической статистике рассматриваются не действия над законами распределения и числовыми характеристиками случайных величин, а приближенные методы отыскания этих законов и числовых характеристик по результатам экспериментов.
Основными понятиями математической статистики являются:
1. Генеральная совокупность;
2. выборка;
3. вариационный ряд;
4. мода;
5. медиана;
6. процентиль,
7. полигон частот,
8. гистограмма.
Генеральная совокупность - большая статистическая совокупность, из которой отбирается часть объектов для исследования
(Пример: все население области, студенты вузов данного города и т.д.)
Выборка (выборочная совокупность) - множество объектов, отобранных из генеральной совокупности.
Вариационный ряд - статистическое распределение, состоящее из вариант (значений случайной величины) и соответствующих им частот.
Пример:
| X,кг | ||||||||||||
| m |
x - значение случайной величины (масса девочек в возрасте 10 лет);
m - частота встречаемости.
Мода – значение случайной величины, которому соответствует наибольшая частота встречаемости. (В приведенном выше примере моде соответствует значение 24 кг, оно встречается чаще других: m = 20).
Медиана – значение случайной величины, которое делит распределение пополам: половина значений расположена правее медианы, половина (не больше) – левее.
Пример:
1, 1, 1, 1, 1. 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 10, 10, 10, 10, 10, 10
В примере мы наблюдаем 40 значений случайной величины. Все значения расположены в порядке возрастания с учетом частоты их встречаемости. Видно, что справа от выделенного значения 7 расположены 20 (половина) из 40 значений. Стало быть, 7 – это медиана.
Для характеристики разброса найдем значения, не выше которых оказалось 25 и 75% результатов измерения. Эти величины называются 25-м и 75-м процентилями. Если медиана делит распределение пополам, то 25-й и 75-й процентили отсекают от него по четвертушке. (Саму медиану, кстати, можно считать 50-м процентилем.) Как видно из примера, 25-й и 75-й процентили равны соответственно 3 и 8.
Используют дискретное (точечное) статистическое распределение и непрерывное (интервальное) статистическое распределение.
Для наглядности статистические распределения изображают графически в виде полигона частот или - гистограммы.
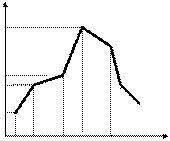
Полигон частот - ломаная линия, отрезки которой соединяют точки с координатами (x1,m1), (x2,m2),..., или для полигона относительных частот – с координатами (x1,р*1), (x2,р*2),...(Рис.1).
 m mi/n f(x)
m mi/n f(x)
X x
Рис.1 Рис.2
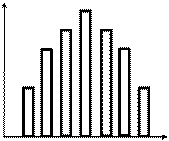
Гистограмма частот - совокупность смежных прямоугольников, построенных на одной прямой линии (Рис.2), основания прямоугольников одинаковы и равны dx, а высоты равны отношению частоты к dx, или р* к dx (плотность вероятности).
Пример:
| х, кг | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 | 4,1 | 4,2 | 4,3 | 4,4 |
| m |






