Эти испытания предназначены для установления соответствия (несоответствия) фактических показателей надежности (безотказности) элементов некоторым нормативным требованиям, задаваемым техническими паспортами, регламентами, отраслевыми стандартами. Контрольным испытаниям подвергают элементы, показатели надежности которых ранее были изучены, но к моменту испытаний могли измениться. Поэтому периодически (для ответственных ТСА через 3-4 года) требуется достаточно быстро и экономно определить фактически существующие в момент t показатели, сравнить их с нормативными величинами и принять решение о надежности или ненадежности элемента.
Методика контрольных испытаний заметно отличается от методики определительных экспериментов. В частности, контрольные испытания проводят на меньшем, чем в определительных опытах, числе элементов; при этом обычно непосредственно испытывают только часть элементов из большой партии однородных элементов; наконец, контрольные опыты прекращаются, как только принимается решение о соответствии или несоответствии показателей надежности элементов нормативным требованиям.
Процедура контрольных испытаний и принятия решений таковы:
Перед испытаниями формируется большая партия однородных элементов, из которой случайным образом составляется небольшая выборка элементов. Эта выборка и подвергается испытаниям, по результатам которых принимается решение о соответствии (или несоответствии) показателей надежности всей партии известным нормативным показателям. Для принятия решения введем так называемую нулевую гипотезу Н0 о том, что по результатам испытаний выборки вся партия удовлетворяет нормативным требованиям (или, проще, "вся партия надежна"). Помимо Н0 существует
альтернативная гипотеза Н1 о том, что по результатам испытаний выборки вся партия ненадежна.
По результатам испытаний и проверке гипотез Н0, Н1 возможна одна из следующих четырех ситуаций.
1. Фактически партия элементов надежна (хотя это и неизвестно); по результатам испытаний выборки принято считать всю партию надежной (т.е. гипотеза Н0 подтверждена). Данное решение – правильное.
2. Фактически партия элементов надежна; по результатам испытаний выборки принята гипотеза Н1 (Н0 случайно не подтвердилась). Принятое решение: считать всю партию элементов ненадежной. Вероятность принятия ошибочного решения (ошибки первого рода или ошибки изготовителя элементов) равна a, 0£a<1. Иногда a называют риском изготовителя. Понятно, что a зависит от величины выборки, точнее, от соотношения объемов выборки и партии.
3. Фактически партия ненадежна, по результатам испытания выборки гипотеза Н0 не получила подтверждения, поэтому принята гипотеза Н1 и решение о ненадежности всей партии. Это решение – правильное.
4. Фактически партия ненадежна, по результатам испытаний гипотеза Н0 "случайно" подтверждена, поэтому принято решение считать всю партию надежной. Это решение ошибочно, здесь допущена ошибка второго рода, невыгодная пользователю элементов. Вероятность этой ошибки (или риска) пользователя обозначают b. Величина b также зависит от объемов выборки и партии.
При контрольных испытаниях всегда имеется желание снизить риски производителя и пользователя a и b. В идеальном случае можно потребовать, чтобы a=0 и b=0. Примем для конкретности за основной контролируемый показатель надежности элемента среднюю наработку tН, и обозначим вероятность приемки партии через F, а нормативный показатель через tНн. Зависимость F от tН получила название оперативная характеристика плана контроля. На рис. 2.37 показана эта характеристика для идеального приемочного контроля F=1.
Рис. 2.37 – Оперативная характеристика идеального приемочного контроля
Если по результатам испытаний проходит гипотеза Н0 (т.е. tН ³ tНн), то вся партия считается надежной с вероятностью F=1 и a=0.
Если tН < tНн, то проходит гипотеза Н1 и вся партия считается ненадежной с вероятностью F=1 и b=0. Идеальная оперативная характеристика не применяется на практике, так как требует полного контроля надежности всех элементов партии сколь угодно большого объема.
Реализуемая оперативная характеристика контроля показана на рис. 2.38
Рис. 2.38 – Реализуемая оперативная характеристика приемочного контроля:
tНa - уровень приемки элемента; tНb - уровень браковки элемента
Если при контрольных испытаниях выполнена гипотеза Н0: tН > tНa, то партия принимается как надежная (с вероятностью не ниже F(tНa)), при подтверждении гипотезы Н1: tН < tНb партия отклоняется как ненадежная с вероятностью не ниже 1-F(tНb). Чем больше зона неопределенности (tНa, tНb), тем меньше нужный объем выборки, но тем больше риски a и b. На практике обычно полагают a=0,1-0,2 и b=0,2-0,3.
Если по результатам испытаний выборки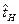 
Î(tНb, tНa), то необходимо продолжить эксперименты на расширенной выборке элементов.
Тактика последовательного контроля иллюстрируется примером испытания выборки из одного восстанавливаемого элемента и заданных малых a и b.
Пусть к моменту t1 зафиксировано n1 отказов элемента и по наработкам между отказами tj, j=1,2,…,N1 найдена оценка 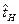. Обычно случайная величина 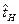имеет нормальное распределение.
Это позволяет найти минимальное число отказов N1-, которое надо наблюдать при контрольных испытаниях элемента, чтобы с заданной вероятностью b не объявить фактически ненадежную партию как надежную. Аналогично определяется максимальное число отказа N1+, которые должны наблюдаться на интервале [0, t1], чтобы с вероятностью a не объявить фактически надежную партию как ненадежную.
Если 
, то контрольные испытания окончены, принимается гипотеза Н0 и вся партия элементов объявляется надежной (вариант a на рис. 2.39).
При N1= 
>N1+ принимается гипотеза Н1 и с вероятностью a партия объявляется ненадежной (вариант б на рис. 2.39).
Возможен и вариант с, когда N1= 
и тогда при N1-< <N1+ контрольные испытания продолжают до некоторого момента времени t2, когда будет зафиксировано N2 отказов и найдена новая, более точная оценка 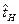и затем вычислены N2-, N2+. Далее снова проводится сравнение N2 с N2-, N2+ с целью принятия одной из гипотез Н0 или Н1 и решения о надежности или ненадежности партии.
Процедура последовательного контрольного испытания выборки из одного восстанавливаемого элемента иллюстрируется рис. 2.39
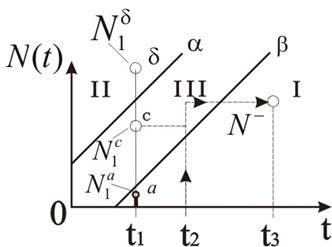
Рис. 2.39 – График последовательных контрольных испытаний элементов.
Здесь:I, II, III – области надежности, ненадежности и неопределенности партии элементов; сплошной тонкой линией показан "след" испытаний элемента (и партии), не прошедшего контрольных испытаний; пунктиром – результаты испытаний элемента, по которым партия признана надежной.
