Самовосстанавливающаяся система "элемент – обслуживающий персонал" часть времени находится в работоспособном состоянии, а часть (иногда значительную) – в состоянии восстановления. Система считается тем лучше, чем больше доля времени, когда она работоспособна или готова к выполнению своих функций. Степень работоспособности системы "элемент – обслуживающий персонал" характеризуется рядом так называемых коэффициентов готовности, косвенно учитывающих безотказность и ремонтопригодность элемента и обслуживающего персонала.
Функция готовности КГ(t) есть вероятность того, что система будет работоспособной в произвольный момент времени t0. Если этот момент времени t0 достаточно удален от нуля и в системе имеет место установившийся или стационарный режим функционирования, то функция готовности КГ(t) превращается в коэффициент готовности КГ, численно равный средней доле времени, когда система работоспособна, от общего времени ее эксплуатации
Для экспоненциальных распределений случайных величин Т и ТВ коэффициент готовности КГ находится по формуле
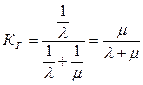
Отметим что стационарный коэффициент готовности КГ не зависит от вида распределений (хотя КГ(t) зависит от распределений Q(t) и Q(tв)) случайных величин Т и ТВ.
Статистическая оценка 
определяется по результатам надежностных испытаний N систем "элемент – обслуживающий персонал":
где N(t0) – число работоспособных систем в "удаленный" момент времени t0. Оценку можно найти и по известным величинам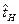 
, 
Коэффициент готовности КГ изменяется от 0 до 1. Если восстановление проводится быстро и tНв малό относительно tН, то КГ®1. Иначе, при длительных ремонтах и низкой безотказности, когда tНв великό, а tН – малό, коэффициент готовности КГ®0. Серийные технические средства автоматизации имеют КГ»0,7-0,9.
В некоторых (немногочисленных) случаях ремонтопригодность и безотказность элемента характеризуют коэффициентом простоя КП:
КП=Вер{того, что элемент находится в ремонте в удаленный момент времени t0}.
Этот стационарный коэффициент простоя определяется через известные tНв и tН
или через КГ
КП=1- КГ
(ибо система "элемент – обслуживающий персонал" находится либо в работоспособном состоянии, либо в ремонте).
Коэффициент оперативной готовности КОГ(t) равен вероятности того, что элемент работоспособен в удаленный момент времени t0 и будет исправным на отрезке времени [t0, t0+t]. Коэффициент КОГ(t) можно выразить через КГ и условную вероятность безотказной работы элемента Р(t0, t) на интервале [t0, t0+t] при условии его исправного состояния в момент t0 .
Для экспоненциального закона вероятность Р(t0, t) не зависит от расположения отрезка t на числовой оси времени, а зависит только от величины t
Р(t0, t)=Р(t)=е-lt
Поэтому для экспоненциально распределенных Т и ТВ коэффициент оперативной готовности равен
Коэффициент КОГ(t) убывает с ростом времени t и почти всегда меньше КГ, только при t=0 имеем КОГ(0)=КГ.
Существует ряд ТСА, которые периодически выводятся на время tПР из эксплуатации, например, для тарировки, профилактики и др. Это время вынужденного "простоя" tПР элемента не связано непосредственно с его безотказностью и ремонтопригодностью и не учитывается при определении tНв и tН, а следовательно, и КГ и КОГ. Если tПР - случайная величина и ее среднее значение М{ tПР } соизмеримо с tНв и tН, то безотказность и ремонтопригодность элемента с вынужденными простоями следует характеризовать коэффициентом технического использования
который всегда меньше КГ.
