Для приближения статистических распределений сложного вида известными ("хорошими") теоретическими распределениями применяют суперпозиции экспоненциальных законов

где: f1(t)=l1×exp{-l1t}, f2(t)=l2×exp{-l2t}, с1,с2 – весовые множители, с1+c2=1; величина с1 подбирается наряду с интенсивностями l1, l2, из условия близости статистической плотности  и нового закона fc(t).
и нового закона fc(t).
Для подобной суперпозиции имеем
Pс(t)= 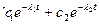
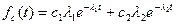
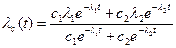
lc(0)= c1l1+ c2l2
Средняя наработка до отказа tНС равна

Вариацией параметров l1, l2, c1 можно добиться хорошей аппроксимации статистических интенсивностей 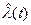 на периодах приработки элемента. Если положить l2>l1, то при малых t функция exp{-l2t} быстрее стремится к нулю, чем exp{-l1t}. Поэтому при больших t имеем lc(t)®l1 (рис. 2.31).
на периодах приработки элемента. Если положить l2>l1, то при малых t функция exp{-l2t} быстрее стремится к нулю, чем exp{-l1t}. Поэтому при больших t имеем lc(t)®l1 (рис. 2.31).
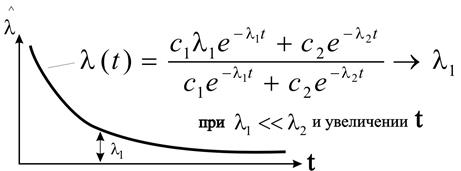
Рис. 2.31 – Суперпозиция двух экспоненциальных распределений
Для описания поведения элементов с внезапными и постепенными отказами применяют суперпозицию экспоненциального и усеченного нормального распределений

где с1+с2=1.
Весовые множители с1, с2 характеризуют частоты внезапных и постепенных отказов. При одинаковой частоте этих отказов с1=с2=0,5. Варьируя с1 (или с2) можно заметно влиять на форму интенсивности lc(t).






