Работоспособность деталей машин характеризуется рядом критериев: прочностью, износостойкостью, жесткостью, теплостойкостью, виброустойчивостью, точностью.
Расчет сводится к сопоставлению по отдельным критериям расчетных параметров с их предельными величинами:
- характеристиками прочности (пределом прочности, текучести, выносливости),
- предельной нагрузкой,
- ресурсом,
- предельными перемещениями (упругими, вызванными износом, температурными),
- теплостойкостью масла и материалов,
- предельными частотами и амплитудами колебаний,
-динамической устойчивостью.
Предельные величины расчетных параметров критерия выбирают по нормативным или справочным данным или устанавливают путем испытаний или наблюдений в эксплуатации.
Работоспособность деталей по заданному критерию обеспечена, если расчетный параметр критерия 
меньше его предельного значения 
. В общем случае параметр не должен выходить за предельное значение.
В настоящее время основное применение имеет расчет с помощью заранее задаваемых коэффициентов безопасности 
, соответственно расчетное условие 
. Величины рассматривают детерминированными, хотя в действительности они могут иметь большой случайный разброс . Расчет приходится вести по наиболее неблагоприятным значениям, когда истинное значение коэффициента безопасности остается неизвестным.
С переходом на вероятностные методы расчета и рассматривают как случайные величины, и мерилом надежности является вероятность безотказной работы 
по заданному критерию. Расчетное условие для обеспечения вероятности безотказной работы в 50% случаев имеет вид 
, а для обеспечения вероятности
,
где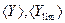 
– средние значения величин и ; 
–среднее квадратичное отклонение разности двух случайных величин и ; 
– среднее квадратичное отклонение величины и ; 
– квантиль нормированного нормального распределения – функция от вероятности .
Здесь, полагают, что разность 
, распределена по нормальному закону, хотя строго это положение выполняется только при нормальных распределениях и ,
Вероятность безотказной работы определяется по заданному критерию в зависимости от величины квантили:
.
Представляет существенный интерес связь квантили , как характеристикой вероятностного расчета, и коэффициентом безопасности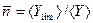 
, рассчитанным по средним значениям. Соответственно разделим числитель и знаменатель дроби на 
и введем коэффициенты вариации 
и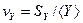 
, тогда
.
Зависимость для параметра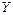 
может быть представлена следующим образом: 
, где 
– случайные факторы. Форма представления зависимости для параметра полностью применима для параметра .
