В этот период постепенные отказы еще не проявляются, и надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность, которая не зависит от возраста изделия 
, где 
; 
– средняя наработка до отказа (обычно в часах). Тогда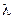 
выражается числом отказов в час и, как правило, составляет малую дробь.
Вероятность безотказной работы
.
Она подчиняется экспоненциальному закону распределения времени безотказной работы и одинакова за любой одинаковый промежуток времени в период нормальной эксплуатации.
Плотность распределения
.
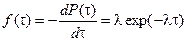Экспоненциальным законом распределения можно аппроксимировать время безотказной работы широкого круга объектов (изделий):
- особо ответственных машин, эксплуатируемых в период после окончания приработки и до существенного проявления постепенных отказов;
- машин с последовательной заменой отказавших деталей;
- машин вместе с электрического и гидродинамического оборудованием и системами управления;
- сложных объектов, состоящих из многих элементов.
При этом время безотказной работы каждого может не быть распределено по экспоненциальному закону. Нужно только, чтобы отказы одного элемента, не подчиняющегося этому закону, не доминировали над другими.
Приведем примеры неблагоприятного сочетания условий работы деталей машин, вызывающих их внезапный отказ (поломку). Для зубчатой передачи это может быть действием максимальной пиковой нагрузки на наиболее слабый зуб при его зацеплении в вершине и при взаимодействии с зубом сопряженного колеса, при котором погрешности шагов сводят к минимуму или исключают участие в работе второй пары зубьев. Такой случай может встретиться только через много лет эксплуатации или не встретиться совсем.
Примером неблагоприятного сочетания условий, вызывающего поломку вала, может явиться действие максимальной пиковой нагрузки при положении наиболее ослабленных предельных волокон вала в плоскости нагрузки.
Существенное достоинство экспоненциального распределения – его простота: оно имеет только один параметр. Расчеты показывают, что для обеспечения требуемой вероятности безотказной работы 0,9 или 0,99 можно использовать только малую долю среднего срока службы (соответственно 0,1 и 0,01).
Если работа изделия происходит при разных режимах, а, следовательно, и интенсивностях отказов 
(за время 
) и 
(за время 
), то
.
Эта зависимость следует из теоремы умножения вероятностей.
Для определения на основании опытов интенсивности отказов оценивают среднюю наработку до отказа 
, где 
– общее число наблюдений. Тогда 
.
