Прогнозирование потребности запасных агрегатов и деталей технологических систем

 

Необходимо проанализировать потребность в запасных частях технологических систем, содержащих n. деталей, за годо­вую плановую наработку 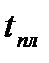при различных наработках групп деталей с начала эксплуатации. Рассчитать эту потребность и выполнить разбивку ее по кварталам в течение года.

При распределении ресурсов заменяемых деталей по нормальному закону величина среднеквадратического отклонения:

 

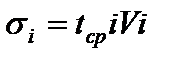, (48)

 

где - средний ресурс i – детали; - коэффициент вариации распределения ресурса.

При любых стратегиях замены отказавших элементов технологической системы процесс восстановления ее по рассматриваемому элементу (детали) или виду ремонта описывается параметром потока отказов (восстановлений).

Параметр потока отказов:

 

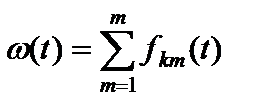, (49)

где – плотность композиции распределений ресурсов конструктивных элементов до m замен.

Ведущая функция потока отказов (восстановлений):

 

, (50)

где - функция композиций распределений ресурсов эле­ментов до m замен.

 

3.3.1. Расчет функций композиций очередных замен, ведущей функции и параметра потока отказов

 

Для большинства технологических систем считают применимым общий процесс восста­новления, при котором ресурс первой детали больше ресурса запас­ной части вследствие ее установки (после выхода из строя первой) в несколько изношенный агрегат.

 

Рис. 3. Функция распределения и вероятность безотказной работы

 

Рис. 4. Плотность распределения вероятностей и интенсивность отказов

Рис. 3.3. функция распределения а вероятность оезотказ» работы

Дня определения функций композиций очередных замен использует­ся общее свойство композиций:

 

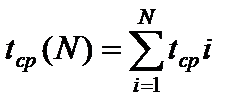, (51)

, (52)

где - средина наработки до первой и последующих замен;

- среднее квадратическое отклонение наработки до первой и последующих замен.

Обычно при общем процессе восстановления наработки второй, третьей и последующих замен принимают 0,8 (80% от наработки первой детали).

Количество замен принять m = 3.

Тогда в соответствии с формулой (51) при первой замене:

 

, (53)

(принимается равной средней наработке, полученной в первой части работы);

при второй замене:

 

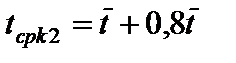, (54)

при третьей замене:

, (55)

Среднее квадратическое отклонение при постоянном значении коэф­фициента вариации при второй и последующих заменах будет состав­лять 0,8 , подученного в первой части работы.

Тогда в соответствии с формулой (52) при первой замене:

 

, (56)

 

принимается равным среднему квадратическому отклонению, получен­ному в первой части работы;

при второй замене:

 

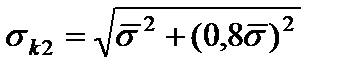, (57)

 

при третьей замене:

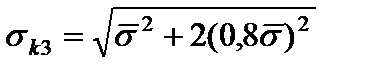, (58)

 

Функции композиций распределения ресурсов элементов до m замен определяют по следующим выражениям:
, значения берутся из графы 12 табл. 2:

 

, (59)

 

, (60)

 

где функция Лапласа определяется по формуле (11).

Для удобства вычислений, все расчетные данные представляются в виде табл. 8, в графы 1...4 которой переносятся результаты из граф 1, 2, 8 и 12 табл. 2.

Максимальное количество необходимых для расчета интервалов определяют следующим образом:

 

, (61)

 

где ;

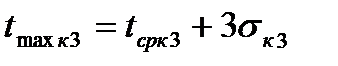- ширина интервала группирования, определенная по формуле (2).

 

Таблица 8