Последовательность вычисления коэффициента асимметрии и эксцесса

 

j		mj		(		(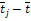

 

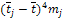
По формуле (24) определить с учетом суммы графы 6 табл. 5 оценку коэффициента асимметрии:

 

. (24)

 

Затем по формуле (25) с учетом суммы графы 8 табл. 5 опре­деляется статистическая оценка коэффициента эксцесса:

 

. (25)

Если значения полученных характеристик невелики (0,04; 0,41), то подтверждается правильность принятой гипо­тезы о виде закона распределения ресурса.

 

3.2.7. Проверка согласия между эмпирическим и теоретическим распределениями по критерии согласия χ² Пирсона

 

Широкое применение критерия χ ² обосновывается легкостью его использования для проверки согласия любого распределения.

Для применения критерия согласия χ ² полученные эмпирические данные группируются по интервалам и сопоставляются с ожидаемым числом наблюдений для принятого закона распределения.

На основе такого сопоставления вычисляется критерий, который приб­лиженно следует распределению χ ² только в том случае, если за­кон описания случайной величины выбран правильно. Если выбор гипо­тезы распределения сделан неправильно, то значение критерия превы­сит значение случайной величины, распределенной по χ ².

Проверка согласия между эмпирическим и теоретическим распреде­лением производится в следующей последовательности:

- определяется число интервалов n, на которые разбиваются полученные эмпирические данные. Все интервалы рекомендуется брать одинаковой длины;

- определяются оценки проверяемого теоретического распределения по группированным значениям , считая их сконцентрированными в средней точке каждого интервала;

- подсчитывается число наблюдений в каждом интервале. Интервалы, в которых встречаемость частот (количество наблюдений) мень­ше 5, объединяются с соседними;

- определяется вероятность попадания в каждый интервал случайной величины, имеющей принятый по гипотезе закон распределе­ния;

- вероятность попадания наблюдений в интервал умножается на объем выборки n, т.е. определяется математическое ожидание числа наблюдений в каждом интервале для принятой теоретической модели;

- вычисляется критерий согласия χ ², Пирсона:

 

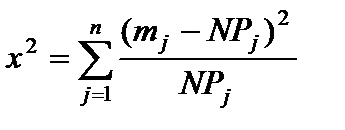, (26)

величина χ ² асимптотически подчиняется распределению χ ² с числом степеней свободы:

, (27)

где l - число параметров теоретического распределения;

- число интервалов после объединения.

Чем меньше полученное значение χ², тем лучше согласие между эмпирическим и теоретическим распределением.

После вычисления χ² задаются доверительной вероятностью:

 

. (28)

 

того, что величина χ² , полученная в результате случайных откло­нений частот эмпирического распределения от соответствующих час­тот теоретического распределения будет меньше табличного значения (χ*)², установленного для выбранной доверительной вероят­ности. Если вычисленное значение χ² будет меньше табличного зна­чения (χ*)², то для принятой доверительной вероятности гипотеза о согласии эмпирического и теоретического распределения не отвергается, в противном случае ее нельзя принять. Таким образом, если вычисленное значение χ² превышает табличное при заданной доверительной вероятности, то принятая теоретическая модель отвергается но в этом случае целесообразно сравнить фактические частоты с ожидаемыми, чтобы увидеть, какие интервалы оказывают наибольшее вли­яние на величину χ². Такое сравнение наглядно показывает ха­рактер отклонения от принятой теоретической модели.

После вычисления χ² можно задаться и уровнем значимости , т.е. вероятностью:

 

. (29)

 

того, что вычисленное значение χ², превысит табличную величину (χ*)². Критическую область образуют все значения χ²>(χ*)². Заключение, что проверяемая гипотеза отвергается, т.е. опытное распределение не соответствует предполагаемому, делают, если вы­численное значение критерия согласия χ ² попадает в критическую область, т.е. χ ² будет больше табличного значения (χ*)², соот­ветствующего выбранному уровню значимости . При значе­нии χ²<(χ*)² гипотеза не отвергается. Уровень значимости может быть принят в пределах (0,01...0,3), значения (χ*)² приведе­ны в табл. 7 приложения.

Для проверки соответствия эмпирического распределения теорети­ческому по критерию χ ² Пирсона переписывают из табл. 2 значения граф 1...3 и 10 в графы 1...4 табл. 6.

Интервалы, в которых встречаемость частот меньше 5, объеди­нить с соседними.

Вычисляется по формуле (30) вероятность попадания эмпирических данных в каждый интервал:

 

. (30)

 

Полученные результаты записываются в графу 5 табл. 6.

Рассчитываются значения показателей и заносятся в графы 6...9 табл. 6. Затем по формуле (3.26) с учетом суммы графы 9 табл. 6 рассчитывается значение критерия согласия χ ² Пирсона.

Задаются доверительной вероятностью и с учетом формул (28) и (29) делают вывод о согласованности эмпирических данных с выб­ранной по гипотезе моделью теоретического распределения.

 

Таблица 6