Полученные значения количественных характеристик показателей надежности в дальнейшем должны быть распространены на другие технологические системы, работающие в условиях, отличных от исследуемых. При этом изменение количества технологических систем в группе и условий их эксплуатации вызовет и изменение количественных показателей надежности. Несмотря на то, что эти изменения носят случайный характер, они происходят в определенных границах или в определенном интервале. Величина этого интервала зависит от многих факторов, в том числе и от количества технологических систем в группе. Определение границ рассеивания характеристик показателей надежности, а следовательно, и определение возможной ошибки их переноса из одних условий в другие является одной из основных задач теории надежности.
Поэтому после того, как вид закона установлен, определяют границы доверительного интервала количественных показателей надежности, и в первую очередь, доверительного интервала значений математического ожидания. Для нормального закона распределения в общих случаях в качестве доверительного интервала принимают интервал, отличающийся от среднего значения показателя на величину 
. Площадь между дифференциальной кривой и осью абсцисс, ограниченная величиной 
, составляет 0,997 или 99,7% всей площади, т.е. в 997 случаях из 1000 значение одиночного показателя (точечной оценки) надежности будет находиться в интервале .
Задаваясь заранее меньшими значениями площади охвата, соответственно сближают границы рассеивания точечной оценки показателя надежности и тем самым уменьшают возможную погрешность расчета, хотя и за счет снижения доверия. При обработке эмпирических данных о надежности технологических систем и их элементов нередко требуется определить не только точечную оценку, но и ее точность и достоверность, т.е. необходимо найти к каким случайным ошибкам может приводить, например, замена параметра его оценкой. Экспериментальная оценка 
является случайной величиной, поэтому можно указать определенную вероятность γ того, что истинное значение параметра α заключено в пределах заданной точности оценки, т.е.:
, (31)
где 
- заданная точность; 
- достоверность оценки (доверительная вероятность).
Характеристики оценивания являются более полными, если оценивать параметр не по одной, а по двум оценкам нижней 
и верхней 
.
Для заданной вероятности 
, по конечной совокупности наблюдений t1, t2,…,tN случайной величины может быть получена такая оценка 
(рис. 2), что интервал от 
до 
накрывает, параметр 
с этой вероятностью :
. (32)
Величина называется нижней доверительной границей параметра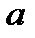 
, а величина - односторонний доверительной вероятностью.
Рис. 2. Доверительные границы
При таких же условиях для заданной вероятности 
может быть получена такая оценка 
(см. рис. 2), что интервал от 0 до 
накрывает параметр 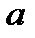с этой вероятностью .
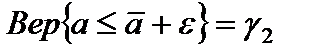, (33)
Величина называется верхней доверительной границей, а величина - односторонней доверительной вероятностью.
Нижняя и верхняя доверительные границы образуют доверительный интервал, который с двусторонней доверительной вероятностью 
накрывает параметр :
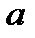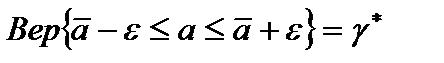, (34)
Двусторонняя доверительная вероятность 
определяется при условии, что , и больше 0,5:
, (35)
Если 
, равенство (35) принимает вид:
, (36)
и тогда односторонняя доверительность вероятность:
, (37)
Величина характеризует достоверность оценки, а величина 
(доверительный интервал) (cм. рис. 2) – точность оценки.
При нормальном законе распределения нижняя и верхняя односторонние доверительные границы параметра 
при заданной доверительной вероятности 
:
, (38)
, (39)
где 
- квантиль распределения Стьюдента для односторонней доверительной вероятности (выбирается по табл. 6 приложения в зависимости от принятого уровня доверительной вероятности и числа степеней свободы К = N - 1).
Для среднего квадратического отклонения σ односторонние доверительные границы вычисляются по формулам:
, (40)
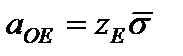, (41)
где 
и 
коэффициенты, рассчитываемые в зависимости от односторонней доверительной вероятности и числа степеней свободы К = N – 1 по уравнениям
, (42)
, (43)
где 
- выбирается по табл. 6 приложения при К <100; и рекомендуется выбирать по таблицам ГОСТ 11.004-74.
