Согласно результатам, полученным в работе [ 7 ], нижняя граница надежности элемента  , прогнозируемая после проведении k испытаний, в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
, прогнозируемая после проведении k испытаний, в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
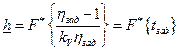 ,
,
где  коэффициент вариации коэффициента параметрического запаса
коэффициент вариации коэффициента параметрического запаса 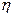 ;
;
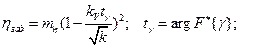
 уровень доверительной вероятности;
уровень доверительной вероятности;
 математическое ожидание коэффициента запаса; k- число испытаний;
математическое ожидание коэффициента запаса; k- число испытаний;
 функция нормированного нормального распределения.
функция нормированного нормального распределения.
Таким образом потребный уровень математического ожидания коэффициента запаса удовлетворяет соотношению
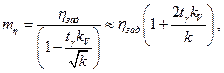
После преобразований будем иметь
 ,
,
Введя обозначения 

 , получим
, получим  .
.
Таким образом  , где
, где  .
.
Следовательно, требуемый уровень надежности может быть подтвержден при различных комбинациях параметров tmi и 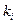 . Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
. Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
Очевидно, уровень избыточности элементов системы tmi будет определять производственные и эксплуатационные расходы на выполнение программы:

где  N – объем выпускаемой продукции;
N – объем выпускаемой продукции;
 коэффициент чувствительности, характеризующий удельные затраты на обеспечение единицы надежности, выраженной в гауссах.
коэффициент чувствительности, характеризующий удельные затраты на обеспечение единицы надежности, выраженной в гауссах.
Параметр 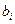 определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы
определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы 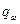 оценивается по соотношению
оценивается по соотношению
 ,
,
где  вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента;  условная кратность резерва.
условная кратность резерва.
Отсюда  .
.
Очевидно стоимость резервированного элемента будет равна
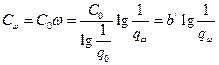 ,
,
где  стоимость нерезервированного элемента;
стоимость нерезервированного элемента;
 вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента;
 затраты на единицу надежности, выраженной в беллах.
затраты на единицу надежности, выраженной в беллах.
Переходя к оценке надежности в гауссах, получим
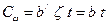 , где
, где  ;
;  .
.
Очевидно параметр b характеризует удельные затраты на единицу надежности, выраженной в гауссах.
Зависимость стоимости от кратности резерва можно представить в виде

 .
.
Вид функции  зависит от типа резервирования.Очевидно, в случае «горячего» резерва, имеем
зависит от типа резервирования.Очевидно, в случае «горячего» резерва, имеем  .
.
. Для «холодного» резерва стоимость резервной группы представим в виде
 ,
,
где m – общее число элементов в резервной группе.
Отсюда  .
.
Для нахождения m воспользуемся приближенной оценкой  [5].
[5].
 .
.
После логарифмирования, получим
 .
.
Характер изменения m по  для различных
для различных  представлен на рис. 2.8
представлен на рис. 2.8

Рис. 2.8 Зависимость числа элементов m в резервной группе от
кратности резерва  .
.
При проведении практических расчетов зависимость  , в реальном диапазоне изменения надежности, можно аппроксимировать прямой
, в реальном диапазоне изменения надежности, можно аппроксимировать прямой
 .
.
В частности, для рассматриваемого случая, получим

В дальнейшем найдем аналогичные соотношения для элементов с параметрической избыточностью. При решении поставленной задачи, вероятность отказа элементов с параметрической избыточностью условно представим в виде

где  - вероятность отказа элемента, соответствующая коэффициенту запаса
- вероятность отказа элемента, соответствующая коэффициенту запаса  ;
;  условная кратность резерва.
условная кратность резерва.
Согласно результатам, полученным в работе [ 7 ], надежность элемента  ,прогнозируемая после проведении k испытаний, может быть оценена по соотношению
,прогнозируемая после проведении k испытаний, может быть оценена по соотношению
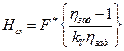 ,
,
где  коэффициент вариации коэффициента запаса;
коэффициент вариации коэффициента запаса;
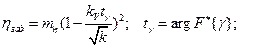
 уровень доверительной вероятности;
уровень доверительной вероятности;
 математическое ожидание коэффициента запаса.
математическое ожидание коэффициента запаса.
Знание  , позволяет оценить условную кратность резерва
, позволяет оценить условную кратность резерва
 ,
,
В дальнейшем будем считать, что стоимость резервированного элемента пропорциональна коэффициенту запаса 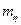 . Тогда функцию
. Тогда функцию  можно оценить по соотношению
можно оценить по соотношению 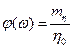 .
.
Характер изменения функции  представлен на рис. 2.9.
представлен на рис. 2.9.

Рис. 2.9 Характер изменения функции  для элементов с параметрической избыточностью.
для элементов с параметрической избыточностью.
При построении графика было приняты следующие исходные данные:
 1.3;
1.3; 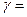 0,95;
0,95;  0,1;
0,1;  2, 5, 10.
2, 5, 10.
Как видно из графика функция  слабо зависит от объема испытаний k. Приближенно для функции
слабо зависит от объема испытаний k. Приближенно для функции  может быть принята линейная аппроксимационная зависимость
может быть принята линейная аппроксимационная зависимость
 .
.
С учетом полученных результатов, выражение для стоимости примет вид
 ,
,
где 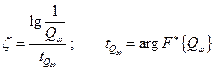
Отсюда
 , где
, где  .
.
Для рассмотренного в примере случая: 
Соответственно затраты на экспериментальную отработку будут определяться объёмами испытаний элементов

где Ci - затраты на проведение одного испытания i-го элемента,
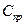 – затраты, не зависящие от варьирующихся параметров.
– затраты, не зависящие от варьирующихся параметров.
Таким образом, решение задачи сводится к минимизации функции суммарных затрат
 (2.36)
(2.36)
В качестве дисциплинирующего условия рассмотрим правую границу неравенства (2.35)
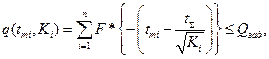
В дальнейшем для нахождения оптимального решения задачи рассмотрим функцию Лагранжа

Оптимальные параметры будут удовлетворять системе алгебраических уравнений:


При нахождении производной  , предполагая, что число испытаний
, предполагая, что число испытаний  существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания
существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания  будем считать постоянными для каждого i-го элемента системы.
будем считать постоянными для каждого i-го элемента системы.
Производя дифференцирование, получим:
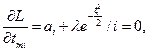
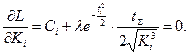 (2.37)
(2.37)
Разрешая систему уравнений относительно Ki, найдем
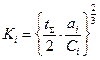 (2.38)
(2.38)
Соотношение (2.38) позволяет оценить оптимальный объем испытаний с точностью до целых. Таким образом оптимальные объемы испытаний отдельных элементов не зависят от требований, предъявляемых к надежности систем и определяются соотношением удельных затрат на обеспечение единицы надежности, закладываемой на этапе проектирования, 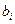 и затрат на проведение одного испытания
и затрат на проведение одного испытания  .
.
Соответственно, из первого уравнения системы (2.37) получим:

где 
Подставляя 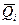 в граничное условие, приходим к соотношению:
в граничное условие, приходим к соотношению:  .
.
Отсюда 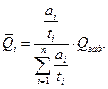 (2.39)
(2.39)
Таким образом, оптимальные уровни вероятности отказа пропорциональны удельным затратам  и заданным требованиям к вероятности отказа системы
и заданным требованиям к вероятности отказа системы  .
.
Заметим, что предположение о постоянстве  , принятое выше, может не выполняться при создании единичных КА, затраты на разработку и экспериментальную отработку которых, существенно превышают затраты на изготовление и применение этих комплексов. Они составляют до 70% от общих затрат на всю программу. В этом случае решение должно быть уточнено.
, принятое выше, может не выполняться при создании единичных КА, затраты на разработку и экспериментальную отработку которых, существенно превышают затраты на изготовление и применение этих комплексов. Они составляют до 70% от общих затрат на всю программу. В этом случае решение должно быть уточнено.






