В случае экспоненциального распределения наработки на отказ надежность элемента равна [ 9 ]
где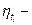 
коэффициент временного запаса.
Очевидно, что
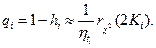
В общем случае надежность технической системы будет определяться уровнями надежности отдельных элементов, входящих в ее состав. При последовательно соединении элементов вероятность отказа технической системы приближенно можно оценить по соотношению
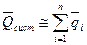где 
.
Отсюда с учетом (3.5) получим
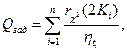(2.40)
где Qзад - заданная вероятность отказа системы.
Следовательно, требуемый уровень надежности системы может подтвержден при различных комбинациях параметров 
и Ki. Среди многообразия значений и Ki целесообразно выбрать те, которые обеспечивают заданный уровень надежности при минимальных затратах.
Очевидно, уровни избыточности элементов системы mti будут определять эксплуатационные расходы на выполнение программы
(2.41)
В дальнейшем для упрощения расчетов введем новую переменную
.
При этом соотношения (3.6), (3.7) примут вид
(2.42)
(2.43)
В линейном приближении соотношение (2.43) можно представить в виде 
Для оценки коэффициента чувствительности 
проанализируем выражение для стоимостных затрат. Очевидно стоимость элемента с избыточностью 
можно представить в виде
,
где 
стоимость нерезервированного элемента с коэффициентом запаса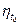 
;
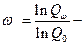кратность резерва;
вероятности отказа соответственно элемента с избыточностью и нерезервированного элемента;
.
В рассматриваемом случае
,
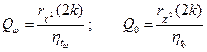где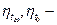 
коэффициенты временного запаса соответственно для
элемента с избыточностью и нерезервированного элемента.
Таким образом кратность резерва 
будет равна
. (2.44)
В дальнейшем воспользуемся приближенной оценкой [ 9 ]
.
где 
аппроксимирующие коэффициенты.
Отсюда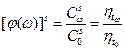 
.
Таким образом
(2.45)
С учетом (2.45) выражение (2.44) примет вид
.
После преобразований, получим
.
Характер изменения 
для 
и s=4 представлен на рис.2.10
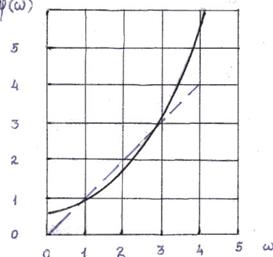
Рис.2.10 Характер изменения функции для элемента с временной избыточностью.
В реальном диапазоне изменения 
кривую можно аппроксимировать прямой .
С учетом полученных результатов, выражение для стоимости элемента с избыточностью примет вид
,
где 
.
Заметим, что при изменении 
от 50 до 300 величина корректирующего множителя 
, для значения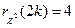 
, меняется в диапазоне 0,65—0,75.
Отсюда для коэффициента получим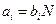 
.
Соответственно затраты на экспериментальную отработку будут определяться объемами испытаний элементов
где Ci – затраты на проведения одного испытания i-го элемента;
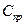– затраты, независящие от варьируемых параметров.
Таким образом, решение задачи нормирования надежности сводится к минимизации функции Лагранжа
где 
; l – неопределенный множитель Лагранжа.
Оптимальные параметры будут удовлетворять системе алгебраических уравнений
Производя дифференцирование, получаем
Разрешая второе уравнение относительно произведения l∙e-Zi и подставляя полученный результат в первое, получаем
Отсюда найдем 
(2.46)
 |
Характер изменения функции
от К для 
представлен на рис.2.11
Рис. 2.11 Зависимость функции 
от числа испытаний.
Полученный результат позволяет проводить оценку оптимального числа испытаний элементов в зависимости от соотношения удельных затрат на эксплуатацию и проведение испытаний.
Соответственно из первого уравнения системы имеем 
Подставляя в граничное условие (3.8), приходим к соотношению
Отсюда 
(2.47)
Таким образом распределение надежности между элементами системы целесообразно проводить пропорционально удельным затратам на обеспечение единицы надежности .
