Для прогнозирования уровня проектной надежности изделий в зависемости от их вида и условий функционирования могут быть использованы два принципиально различных подхода, обоснование которых дается соответственно формальной теорией надежности и общей теорией.
В формальной теории принято, что изменение надежности во времени подчинено некоторым статистическим зависимостям, которые определяются лишь из эксперимента. Физическая сущность причины отказа в этом случае не выясняется.
Формальная теория надежности обычно используется при расчете надежности радиоэлектронной аппаратуры, электромеханических агрегатов и механизмов, работоспособность которых определяется по снашиваемости. В этом направлении работали такие видные ученые как Борг, Гнеденко, Сотсков и другие.
Основные количественные характеристики надежности в этом случае связаны со временем работы изделия и определения из большого числа экспериментов. К ним относятся:
1. Среднее время функционирования изделия - Т;
2. Интенсивность отказа – 
3. Вероятность безотказного функционирования изделия в течение заданного промежутка времени – Р(t)
Поясним более подробно смысл второй характеристики – . Согласно определению, под интенсивностью отказа понимается вероятность того, что изделие, проработавшее до момента времени t, откажет в следующую единицу времени.
Применение тех или иных показателей зависит от конкретной постановки задачи. Так при оценки эффективности поражения цели нас интересует вероятность выполнения задачи, а следовательно, в качестве показателя надежности надо рассматривать вероятность безотказного функционирования изделия.
В то же время при оценке эффективности функционирования орбитального комплекса нас может интересовать среднее время его безотказного функционирования - Т, то есть первая характеристика. Между тремя рассмотренными характеристиками существует взаимнооднозначное соответствие, то есть они могут быть выражены друг через друга. Для нахождения этого соответствия проанализируем возможное состояние изделия в процессе функционирования. Очевидно, их всего два: 1 – работоспособное, 2 – состояние отказа. Причем, в процессе функционирования возможны переходы из первого состояния во второе с интенсивностью. Граф состояний для рассматриваемого случая представлен на рис. 1.2. В дальнейшем оценим вероятность события А, состоящего в том, что изделие находиться в работоспособном состоянии в момент времени t + 
t. Очевидно для этого необходимо выполнения двух событий, а именно: события В, состоящего в том, что изделие находиться в первом состоянии в момент t, событие С, состоящего в том, что в течение отрезка t не произойдет отказа. Тогда используя теорему умножения, получим
(1.1)
Учитывая принятые обозначения соотношение (2.1) можно записать так
 |
(1.2)
С другой стороны, согласно определению λ, вероятность отказа изделия на отрезке Δt при условии его безотказного функционирования до момента t равна λΔt. Отсюда, условная вероятность P{C/B} его безотказного функционирования на отрезке Δt, как вероятность противоположного события будет равна (1 – λΔt).
Таким образом, соотношение (1.2) примет вид
P1{t + Δt} = P1{t}(1 – λΔt) (1.3)
После преобразований получим
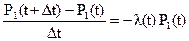(1.4)
Переход к пределу при Δt → 0, приходим к дифференциальному уравнению
 |
(1..5)
или
Интегрируя, получим
 |
(1..6)
Отсюда
 |
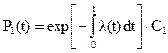(1..7)
где С1 = Р1(0) – вероятность исправности изделия в начальный момент времени.
Соотношение (1..7) позволяет оценить надежность изделия при любых заданных λ(t). В частном случае постоянство интенсивности отказа (λ(t) = λ = соnst) выражение (1..7) упростится
(1.8)
Этот случай соответствует так называемому экспоненциальному закону надежности и находит широкое рассмотрение на практике. Действительно для многих технических условий кривая изменений λ(t) имеет «ваннообразный вид» (см. рис. 1.3). Таким образом, весь период функционирования может быть разбит на три участка: период приработки, штатного функционирования и период старения. Как правило, крайние участки не рассматривается при оценке надежности, так как приработочные отказы устраняются при контрольных проверках, а участок старения исключается соответствующим назначением ресурса.
Третья характеристика, среднее время безотказной работы, находиться как математическое ожидание времени отказа
(1..9)
где f(t) – плотность распределение времени отказа.
Для экспоненциального закона соотношение (2.9) примет вид
 |
(1.10)
Приведенные результаты показывают, что при изменении интенсивности отказа λ нахождение основных показателей надежности не представляет особого труда. Значения λ определяются статистически и приводятся в соответствующих справочниках.
