Основные аспекты, задачи и модели технической диагностики

 

Выше указывалось, что в простейшем случае определение предмета исследования предполагает задание объекта и схемы предмета. Однако на самом деле чаще всего имеет место более сложная ситуация. Усложнение может заключаться в том, что непосредственно исследуется не исходный объект, а некоторая его идеализированная модель.

Замена исходного объекта моделью связана в первую очередь с вы­делением основных существенных сторон исследуемых явлений и с их уп­рощением, позволяющим дать их математическое описание.

Построение идеализированных моделей приводит к расщеплению схемы предмета исследования и к выделению двух групп задач. С одной стороны, это схемы и задачи при исследовании исходного объекта. Здесь речь идет об исследовании параметров, знание которых необходимо при построении модели. С другой стороны, это схемы и задачи при использо­вании модели.

Используя вышеприведенные общие соображения, можно выделить в технической диагностике следующие три основных аспекта:

1) изучение конкретных объектов диагностики;

2) построение и изучение соответствующих математических моде­лей;

3) исследование диагностических систем и их связей с объектом ди­агностики.

Эти аспекты отличаются друг от друга как по непосредственному предмету исследования, так и по используемым методам.

Первый аспект технической диагностики связан с разработкой мето­дов решения и решением таких основных задач, как:

– изучение нормального функционирования системы;

– выделение элементов системы и связей между ними;

– выделение возможных состояний системы, т.е. возможных комби­наций отказов элементов;

– анализ технических возможностей контроля признаков, характери­зующих состояние системы;

– сбор и обработка статистических материалов, позволяющих опре­делить распределение вероятностей возможных состояний системы, а также закономерности проявления отказов отдельных ее элементов;

– сбор экспериментальных данных о затратах, связанных с осущест­влением этих проверок.

Все эти задачи предполагают для своего решения эмпирическое ис­следование конкретных технических систем и процедур диагностики.

Второй аспект технической диагностики связан с построением мате­матических моделей объектов и процессов диагностики и, следовательно, с решением таких задач, как:

– построение математических моделей объекта диагностирования, адекватно описывающих его поведение в исправном и неисправном со­стоянии;

– разработка методов построения диагностических тестов при поиске отказавших элементов;

– построение оптимальных программ диагностики, т.е. последова­тельностей проверок, позволяющих определить состояние технической системы методом последовательного поиска.

Эти задачи носят в основном математический характер. Их решение, полученное для конкретной технической системы, дает возможность опре­делить ее состояние с минимальными затратами, т.е. наилучшим образом по отношению к заданному критерию. При автоматизации процесса диаг­ностики программа должна служить основой для разработки алгоритма функционирования диагностической системы.

Формализация методов построения алгоритмов диагностирования технического состояния некоторого объекта предполагает наличие фор­мального описания объекта и его поведения в исправном и неисправном состояниях. Такое формальное описание (в аналитической, табличной, векторной, графической или другой форме) будем называть математиче­ской моделью объекта диагноза. Математическая модель объекта диагноза может быть задана в явном или неявном виде.

Явная модель объекта диагностирования представляет собой сово­купность формальных описаний исправного объекта и всех (точнее, каж­дой из рассматриваемых) его неисправных модификаций. Для удобства обработки все указанные описания желательно иметь в одной и той же форме. Неявная модель объекта диагноза содержит какое-либо одно фор­мальное описание объекта, математические модели его физических неис­правностей и правила получения по этим данным всех других интересую­щих нас описаний. Чаще всего заданной является математическая модель исправного объекта, по которой можно построить модели его неисправных модификаций.

Приведем пример явной модели дискретного объекта диагностиро­вания, заданной в табличной форме. Обозначим множество технических состояний объекта символом Е. Пусть е Î Е обозначает исправное состоя­ние объекта, а е_i Î Е – его i -неисправное состояние. Каждому i -неисправ­ному состоянию соответствует неисправность s_i из множества S и наобо­рот.

Построим прямоугольную таблицу, строкам которой поставим в со­ответствие допустимые элементарные проверки p _i из множества P, а столбцам – технические состояния объекта из множества Е или, что то же, функции Y и Y ⁱ, i = 1, 2, …, | S |, реализуемые объектом, находящимся в ис­правном е или i -неисправном е_i состоянии (табл. 4.1). Будем в дальнейшем значение индекса i = 0 относить к столбцу исправного состояния е. В клетке (i, j) таблицы, находящейся на пересечении строки p _j и столбца е_i, проставим результат 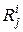элементарной проверки p _j объекта, находящегося в техническом состоянии е_i. Множество всех результатов 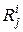, j = 1, 2, …, |P|; i = 0, 1, …, | S | обозначим символом R. Построенную таблицу будем называть таблицей функций неисправностей объекта диагноза [2].

 

Таблица 4.1

 

R	Е
E	…	ei	…	e|S|
P	p1	R 1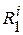
. . .
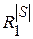
p j	Rj
. . .
p|P|	R |P|

 

Кроме того, модель может быть задана в виде таблицы из нулей и единиц, столбцы которой соответствуют различным возможным провер­кам, а строки – возможным состояниям системы. На пересечении i -го столбца и k -й строки такой таблицы стоит единица, если i -я проверка дает положительный результат, когда система находится в k -м состоянии, и нуль, если i -я проверка дает отрицательный результат. Очевидно, что эти оба вида моделей эквивалентны, и выбор способа задания определяется лишь удобством анализа модели.

Общее требование к моделям исправного объекта и его неисправных модификаций, а также к моделям неисправностей состоит в том, что они должны с требуемой точностью описывать представляемые ими объекты и их неисправности. В неявных моделях объекта диагностирования модели неисправностей, кроме того, должны удовлетворять требованию удобства их «сопряжения» с имеющимся описанием объекта и тем самым обеспечи­вать достаточно простые правила получения других описаний объекта.

Модель объекта диагноза – это формальное описание поведения объ­екта в исправном и неисправных состояниях.

Наиболее распространены следующие виды моделей объекта:

1. Математическая (формула, например, передаточная функция).

2. Структурно-логическая (элементы и связи между ними).

3. Функциональная (список выполняемых функций, например, сис­тема команд процессора).

Модель дефекта для каждой модели объекта своя.

1. Для математической модели объекта моделью дефекта может слу­жить формула с измененными параметрами или переменными.

2. Для структурно-логической схемы общепринята константная мо­дель дефекта. В ней рассматриваются не функции элементов, а только ли­нии связи. На любой линии связи может появиться константа (0 или 1), вне зависимости от того, что подаётся на входе (рис. 4.3). Это может являться следствием обрыва связи, выхода из строя элемента, короткого замыкания и т.д.

Рис. 4.3. Структурно-логическая схема с константами на линиях связи

 

3. Для функциональной модели объекта разрабатывается функцио­нальная модель дефекта, описывающая возможные искажения функциони­рования объекта. В качестве примера рассмотрим систему команд процес­сора.

Пусть K_i – команда на языке низкого уровня, например, ассемблера. Тогда возможны следующие искажения функционирования:

· K_i →0 – команда не выполняется.

· K_i → K _j – заданная команда перешла в другую.

· K_i → υ K_j – вместо K_i выполняется некая совокупность команд.

Исправный или неисправный объект может быть представлен как динамическая система, состояние которой в каждый момент времени t оп­ределяется значениями входных, внутренних и выходных координат (па­раметров). Частным является случай, когда состояние объекта не зависит от времени.

Обратим внимание на то, что термин «состояние объекта» (как ди­намической системы), обозначающий совокупность значений параметров объекта в определенный момент времени, не следует смешивать с терми­ном «техническое состояние объекта», обозначающим наличие или отсут­ствие неисправности в объекте.

Объекты диагностирования разделим на классы. Объекты, все коорди­наты которых могут принимать значения из континуальных мно­жеств значений, отнесем к классу непрерывных объектов. К классу дис­кретных объектов причислим объекты, значения всех координат которых задаются на конечных множествах, а время отсчитывается дискретно. Если значения части координат объекта заданы на континуальных, а значения других – на конечных множествах, то объект является гибридным. В по­следующих разделах данной главы нами рассматривается проблема техни­ческого диагностирования сложных гибридных систем.

Дискретные объекты будем называть комбинационными,или объек­тами без памяти, если значения их выходных координат однозначно опре­деляются только значениями их входных координат. Последовательност­ными, или объектами с памятью, являются объекты, у которых наблюда­ется зависимость значений их выходных координат не только от значений входных координат, но и от времени их поступления на вход ДУ (предыс­тория входных последовательностей во времени). Часто входные и внут­ренние координаты объекта называют входными и, соответственно, внут­ренними переменными, а выходные координаты – выходными функциями.

Обозначим символом Х n -мерный вектор, компонентами которого служат значения n входных переменных х ₁, х ₂, …, х_n. Аналогично Y явля­ется m -мерным вектором значений m внутренних переменных y ₁, y ₂, …, y_m, а Z – k -мерным вектором значений k выходных функций z ₁, z ₂, …, z_k.

Запись

(4.1)

 

будем рассматривать как некоторую аналитическую, векторную, графиче­скую, табличную или другую форму представления системы передаточных функций исправного объекта диагностирования, отражающих зависимость реализуемых объектом выходных функций Z от его входных переменных Х, начального значения Y _нач внутренних переменных и от времени t. Сис­тема (4.1) является аналитической математической моделью исправного объекта [1].

Выделим для рассмотрения конечное множество возможных неис­правностей объекта. Принято различать одиночные и кратные неисправно­сти. Под одиночной понимается неисправность, принимаемая в качестве элементарной, т.е. такой, которая не может быть представлена (или не подлежит представлению) совокупностью нескольких других, более «мел­ких» неисправностей. Кратная неисправность является совокупностью одновременно существующих двух или большего числа одиночных неис­правностей. Символом S будем обозначать множество всех рассматривае­мых (не обязательно всех возможных) одиночных и кратных неисправно­стей объекта, а символом О – множество его одиночных неисправностей. Очевидно, О Í S. Будем говорить, что при наличии в объекте неисправно­сти s_i Ì S, i = 1, 2, …, | S | (или o_i Ì O, i = 1, 2, …, | O |) он находится в i -неис­правном состоянии или является i -неисправным.

Объект диагноза, находящийся в i -неисправном состоянии, реали­зует систему передаточных (характеристических) функций

 

, (4.2)

 

представленных в той же форме, что и передаточные функции (4.1). Заме­тим, что начальное значение Y ⁱ _нач внутренних переменных i -неисправного объекта может не совпадать с их начальным значением Y _нач в исправном объекте. Система (4.2) для фиксированного i является математической моделью i-неисправного объекта.

Другой класс моделей – это модели, учитывающие структуру сис­темы. Их можно разбить, в свою очередь, на две группы в зависимости от того, как именно учитывается эта структура: в одном случае (функцио­нальная модель) она учитывается неявно, в другом (структурная и струк­турно-функциональная модель) – явно.

В первом случае (функциональная модель) при задании модели ука­зываются воздействия, которые должны быть приложены к внешним вхо­дам системы, и функциональные связи между воздействиями и реакциями, наблюдаемыми на внешних выходах системы в зависимости от состояния системы. Любая возможная для данной модели проверка состоит в опреде­лении реакции системы на заданное воздействие.

Во втором случае (структурная, структурно-функциональная модель) модель объекта диагностики основывается на том, что диагностируемую систему рассматривают как конечное множество связанных между собой элементов. Каждый элемент системы отвечает определенной реакцией на приложенную к нему совокупность воздействий, в число которых могут входить реакции других элементов. Воздействия и реакции, которые могут появиться в процессе нормального функционирования системы, т.е. когда все эти элементы работоспособны, называются допустимыми. Реакция от­казавшего элемента при любых условиях является недопустимой. Появле­ние недопустимой реакции на выходе хотя бы одного элемента свидетель­ствует о неработоспособности системы в целом. Два элемента системы связаны между собой, если реакция первого элемента является воздейст­вием для второго и если недопустимая реакция первого элемента вызывает недопустимую реакцию второго независимо от состояния второго эле­мента и от остальных воздействий, приложенных к нему. Каждая возмож­ная для этой модели проверка состоит в контроле реакции одного из эле­ментов системы на определенную совокупность воздействий. Для задания рассматриваемой модели необходимо указать множество элементов, мно­жество возможных состояний системы и схему объекта, отражающую связи между элементами.

Для аналоговых объектов диагностирования под параметрами, опре­деляющими техническое состояние объекта диагностирования, будем по­нимать: простые физические величины – давление, температуру, напряже­ние и т.п.; функции от этих величин, если показатели работоспособности системы или ее элементов имеют интегральный характер; статистические характеристики измеряемых величин или их функций. Для получения по­следних характеристик и расчета величины параметра, являющегося функ­цией некоторой совокупности физических величин и непосредственно не измеряемого или не контролируемого, в состав диагностических систем включают вычислительную часть.

Существуют и другие признаки, которые позволяют сделать класси­фикацию моделей более детальной. Например, при построении моделей могут учитываться или не учитываться такие показатели, как сведения о затратах (время, стоимость) на выполнение отдельных проверок, достовер­ность результатов этих проверок, распределение вероятностей возможных состояний системы и т.д.

В рамках анализа задач выделенного в начале второго аспекта тех­нической диагностики введем ряд понятий, используемых при оптимиза­ции процедуры поиска дефектных элементов и восстановления работоспо­собности объекта диагностирования.

Состояние элементов системы определяется путем выполнения не­которой последовательности проверок, входящих в программу диагно­стики. Проверка включает в себя совокупность операций, производимых над объектом диагностики с целью получения некоторого результата, по которому можно судить о состоянии по крайней мере одного элемента системы. В число основных операций, выполняемых при осуществлении проверки, входит контроль признаков, характеризующих состояние сис­темы в целом или ее элементов.

Совокупность проверок, достаточная для выявления всех заранее за­данных различимых состояний системы, именуется диагностическим тестом.

На рис. 4.4 приведен пример устройства, которое может служить объектом диагностики. Оно состоит из четырех элементов и реагирует оп­ределенным образом на совокупность первичных воздействий S ₁ и S ₂. Эле­менты обозначены строчными буквами, а их реакция – соответствующими прописными буквами.

Система работоспособна, если при входных воздействиях S ₁ и S ₂ она имеет на выходе сигналы В и D, в противном случае она находится в со­стоянии отказа. Аналогично, каждый элемент считается работоспособным, если он реагирует указанным образом на заданные нормальные воздейст­вия. Отказ системы в целом может быть обусловлен отказом одного или нескольких элементов.

 

Рис. 4.4. Пример объекта диагностики

 

В состав операций, осуществляемых при проведении проверок, мо­жет входить специальная подача воздействия на входы системы (ее блоков или элементов). Эти воздействия называют тестовыми, стимулирующими или просто стимулами. В подразд. 2.4 поименованы два класса систем кон­троля – внешние и встроенные.

Можно различать два вида стимулирующих воздействий в зависи­мости от проведения диагностики в процессе нормальной эксплуатации технической системы или при переводе системы в режим тестовой диагно­стики. В первом случае (встроенный функциональный контроль) это есте­ственные (рабочие) сигналы, поступающие на входы исследуемой системы от внешней среды или другой системы. В такой ситуации возникает задача правильного использования имеющихся входных рабочих сигналов. Трудность заключается в том, что возможность управления составом и ве­личиной этих сигналов либо ограничена, либо не существует вовсе. Во втором случае (система тестового диагностирования) в диагностической системе должны быть предусмотрены специальные генераторы стимулов (тестов). При этом объект контроля выведен из рабочего режима и переве­ден в режим технического диагностирования.

Определение реакций объекта диагностики производится путем сравнения текущих значений выходных параметров с их заданными значе­ниями. Для этой цели используются системы технического диагностирова­ния (СТД).

Если не оговорено противное, то под числом состояний диагности­руемой системы будем подразумевать число неработоспособных состоя­ний. Пусть число элементов модели системы равно N. Тогда при независи­мых отказах элементов необходимо учитывать возможность отказа любого сочетания элементов, т.е. возможное число состояний системы есть 2 ^N – 1. Однако часто отказ одного из элементов либо исключает отказ некоторых элементов, либо с необходимостью влечет за собой отказ ряда других эле­ментов. В этих случаях при построении модели объекта диагностики необ­ходимо заранее знать такого рода связи между отказами.

Очевидно, что число состояний системы будет заключено между N и 2 ^N – 1. С практической точки зрения важен еще один случай. Если объект диагностики имеет в своем составе некоторое встроенное контролирующее устройство (встроенная система контроля), которое сигнализирует об от­казе всей системы практически мгновенно, а во многих случаях и отклю­чает систему, то обычно предполагается, что в системе может отказать только один (любой) элемент. Действительно, с одной стороны, для того чтобы неизбыточная система отказала, достаточен отказ лишь одного ее элемента. С другой стороны, с достаточной степенью точностью можно считать вероятность отказа более чем одного элемента за время срабаты­вания встроенного устройства контроля пренебрежимо малой.

Таким образом, в описанной ситуации (наиболее часто используемой на практике) есть основания различать лишь N неработоспособных состоя­ний системы – по числу ее элементов. Очевидно, что в задачах техниче­ской диагностики не имеет смысла говорить о числе состояний отказавшей системы, меньшем N, так как каждый элемент может быть неработоспо­собным.

Для оптимизации вероятностных процедур поиска неисправностей (дефектов) или восстановления работоспособности, учитывающих стати­стическую природу возникновения отказов, в модели объекта должны быть заданы вероятности отказов элементов. Эти вероятности отказов можно рассчитать по характеристикам надежности элементов. Вначале для простоты предположим, что элементы модели соответствуют функцио­нальным элементам исследуемого объекта, причем характеристики их на­дежности известны. Тогда по окончании периода приработки закон рас­пределения случайных отказов элементов наиболее часто описывается экспоненциальным законом:

 

, (4.3)

 

где p_i – априорная вероятность отказа i -го элемента; l _i – интенсивность от­казов i -го элемента в данных условиях его работы; t_i – время работы i -го элемента до его отказа.

Для небольших l t можно считать e^{–l t}» 1– l t и, следовательно,

 

, (4.4)

 

Таблицы интенсивности отказов l _i обычно приводятся в руково­дствах по надежности. Если i -й элемент модели соответствует k_i элементам или деталям, то его вероятность отказа можно найти исходя из известных характеристик k_i реальных элементов. Так как отказ реального элемента модели соответствует отказу хотя бы одного реального элемента, то

 

, (4.5)

 

где индекс k соответствует параметрам реальных элементов.

Как нетрудно видеть, для малых l t

. (4.6)

 

Определение состояния, в котором находится исследуемая система, производится рядом проверок системы.

Перейдем к рассмотрению третьего аспекта технической диагно­стики. Необходимость его введения обусловлена автоматизацией поиска отказавших элементов, построением особых диагностических систем. Если первый аспект связан с эмпирическим изучением объектов диагностики, а второй – с построением и исследованием их математических моделей и процедур диагностирования, то третий аспект – это исследование диагно­стических систем и их связей с объектом диагностики. Этот аспект пред­полагает выполнение описаний существующих диагностических систем, выявление принципов их построения и разработку методов решения, оценку диагностических систем по быстродействию, надежности, избы­точности информации, достоверности диагноза и т.д.

Весьма большое значение имеет разработка методики оценки целе­сообразности и экономической эффективности автоматизации процесса диагностики. Это объясняется тем, что во многих случаях автоматически действующие диагностические системы по своей сложности превосходят диагностируемые объекты. Такие системы зачастую оказываются недоста­точно надежными и экономически малоэффективными. Разработка мето­дики их оценки позволит в каждом конкретном случае определить разум­ную степень автоматизации процесса диагностики и выбрать соответст­вующий принцип действия диагностической системы.

Очень часто современные технические системы проектируются без учета требований диагностики, т.е. требований контролепригодности про­ектируемых объектов. В результате этого ухудшается управляемость и на­блюдаемость объектов и, как следствие, резко усложняется процедура синтеза тестов обнаружения и локализации дефектов и снижения эффек­тивности процесса диагностирования. Это проявляется, главным образом, в отсутствии необходимого числа контрольных точек или в недостаточно удобном их расположении. Учет требований диагностики приводит порой к существенным изменениям схемного решения проектируемых техниче­ских систем. Во всяком случае очевидно, что автоматизация процесса ди­агностики требует, в свою очередь, специальной организации технических систем, допускающей быстрое и удобное присоединение диагностических систем. Поэтому важное значение имеет разработка научно обоснованных рекомендаций, учет которых уже на этапе проектирования технических систем позволит выбирать принцип действия системы, отвечающей требо­ваниям технической диагностики.

Таким образом, автоматизация процесса диагностирования приводит к появлению нового объекта исследования. Этот объект – система диагно­стики. Надо подчеркнуть, однако, что подход технической диагностики к изучению этого нового объекта в корне отличен от того, который был опи­сан выше при изучении объекта диагностирования. Здесь выделяется со­всем другой предмет исследования. Если объект диагностики представляет интерес только со стороны закономерностей появления и обнаружения от­казов, то диагностическая система изучается с точки зрения принципов ее организации и функционирования, с точки зрения критериев оценки ее эффективности.

Взаимная связь выделенных аспектов технической диагностики представлена схемой (рис. 4.5).

Рис. 4.5. Основные аспекты технической диагностики

 

 

Здесь О – объект диагностики; М – модель объекта; П – результаты исследования модели, например оптимальная программа поиска и т.д.; ДС – диагностическая система; ОС – описание и оценка диагностической сис­темы. Цифры обозначают соответственно: 1 – процедуры эмпирического исследования объектов диагностики и построение математических моде­лей; 2 – исследование моделей; 3 – конструирование и построение диагно­стических систем; 4 – процедуры описания и оценки диагностических сис­тем; 5 – конструирование и построение технических систем как потенци­альных объектов диагностики.

На схеме видно, что продукты эмпирического и математического ис­следования объектов диагностики ложатся в основу конструирования и по­строения диагностических систем.

В свою очередь, продукты описания и оценки этих систем сущест­венно влияют на характер исследования объектов диагностики. Ни одна модель, например, не учитывает и не может учитывать всех возможных причин неработоспособности технического устройства. Степень упроще­ния и идеализации диктуется, в частности, учетом стоимости и экономиче­ской эффективности диагностических систем.

 

4.1.3. Классификация диагностических процедур ­­и их краткая характеристика

 

Различают два основных метода поиска отказавших элементов (ди­агностических процедур) – комбинационный и последовательный.

При использовании первого метода (комбинационный поиск) со­стояние системы определяется путем выполнения заданного числа прове­рок, порядок осуществления которых безразличен. Выявление отказавших элементов производится после проведения всех заданных проверок. С этой целью сопоставляются (анализируются) результаты проверок. Для этого метода характерны ситуации, когда не все результаты выполненных про­верок необходимы для определения состояния системы.

При использовании второго метода (последовательный поиск) диаг­ностики оптимизация процедуры последовательного поиска производится в общем случае двумя путями:

1) выбором необходимых проверок и восстановительных операций из всего множества заданных;

2) определением рациональной последовательности их выполнения.

Модели объектов диагностики, для которых строятся исключительно последовательные процедуры, удовлетворяют таким ограничениям:

1. В диагностируемой системе возможны лишь поэлементные про­верки и общая проверка системы, устанавливающая факт работоспособно­сти или отказа всей системы.

2. Отказы элементов независимы, т.е. определение работоспособно­сти или отказа какого-либо элемента не «деформирует» распределение ве­роятностей отказов отдельных элементов.

Использование таких моделей целесообразно в двух случаях: в ис­следуемом объекте связи между выделенными элементами практически отсутствуют или использование этих связей для целей диагностики за­труднительно либо ввиду многочисленности этих связей, либо из-за слу­чайного характера связей, либо по каким-то иным причинам.

И наконец, поскольку многие сложные системы состоят из большого числа однотипных элементов, использование в разумных пределах поэле­ментных проверок упрощает конструкцию автоматических испытательных установок и используемые алгоритмы.

Будем говорить о двух видах процедур последовательного поиска (программ диагностики) – безусловной и условной. Под безусловной про­цедурой будем понимать такую, при которой порядок проведения поверок определяется заранее, до начала поиска, и в процессе поиска остается не­изменным. Если же проверка на некотором j -м шаге назначается в зависи­мости от предыдущих j –1 проверок, то такую последовательную проце­дуру назовем условной. Вообще говоря, безусловная программа поиска есть частный случай условной.

Методы диагностики технического состояния систем можно поде­лить на детерминированные и вероятностные. Детерминированные методы можно поделить на методы с условной процедурой локализации дефектов и методы с последовательной процедурой локализации дефектов, а вероят­ностные методы – на методы локализации дефектов с использованием ап­парата экспертных систем, методы с последовательной процедурой лока­лизации дефектов (при этом на модель накладываются определенные огра­ничения) и методы с условной процедурой локализации дефектов (рис. 4.6).

Одной из широко применяемых на практике процедур технического диагностирования состояния сложных систем (в том числе и гибридных) является поиск отказавших элементов (устройств) и восстановление рабо­тоспособности методом замены элементов. Для указанной процедуры ха­рактерно использование описанных выше моделей. Суть метода состоит в следующем. Используя возможности поэлементной проверки устройств (узлов), определяют техническое состояние i -го элемента. Если проверяе­мый элемент исправен, то в соответствии с принятым критерием определя­ется следующий проверяемый элемент, иначе забракованный элемент за­меняется на исправный и производится переход к следующему шагу про­цедуры (выбору очередного проверяемого элемента).

 

 

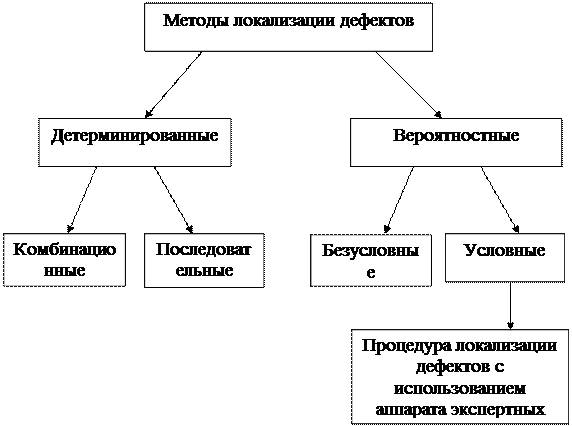
Рис. 4.6. Классификация процедур поиска и локализации дефектов

 

Простейшей разновидностью описываемой процедуры является сле­дующая. В случае отрицательной реакции на выходе диагностируемой системы i -й подозреваемый элемент (i -й шаг процедуры) без проверки его технического состояния заменяется на заведомо исправный. Если система переходит в работоспособное состояние, то дефект считается обнаружен­ным, если нет – производится замена следующего элемента или блока. Таким образом, если до проведения некоторой проверки было известно, что система находится в одном состоянии из некоторого подмножества S ^k, то после проведения проверки можно указать подмножество S ^l, в одном из состояний которого находится система, причем S ^l Í S ^k.

Каждой проверке приписывается стоимость, отражающая затраты труда, времени, затраты на необходимую аппаратуру и т.д. Стоимость дан­ной проверки является суммой стоимостей элементарных операций, ее со­ставляющих, и, вообще говоря, зависит от того, какие проверки ей предшествовали. Поэтому последующие проверки, если при их выполнении используются ранее выполненные операции, могут иметь пониженную стоимость. Практические оценки стоимостей проверок сводятся к анализу стоимостей элементарных операций данной проверки.

Итак, при построении процедуры поиска отказов и восстановления работоспособности методом замены элементов, как уже было сказано выше, различают вероятностную и детерминированную диагностику. Если в модели объекта предполагается, что операция восстановления элементов производится лишь после установления факта их неработоспособности с вероятностью, равной 1, то будем говорить, что модель предполагает де­терминированную диагностику. В этом случае средние затраты на восста­новление работоспособности элементов зависят лишь от затрат на восста­новление каждого элемента и вероятности обнаружения его отказа и не за­висят от последовательности проверок. Следовательно, при оптимизации процедуры стоимости восстановления элементов могут быть исключены из рассмотрения. Поскольку в практике обслуживания технических систем довольно часто применяется детерминированная диагностика, оптими­зации собственно поиска отказов уделяется большое внимание.

Если же проверка и замена элемента в случае обнаружения его от­каза производятся на основании распределения вероятностей отказов, при­чем эти вероятности могут быть не равны 1, то такую диагностику назовем вероятностной. Упомянутое распределение вероятностей строится исходя из информации, полученной при проверках и заменах элементов. Отличи­тельной чертой вероятностной диагностики методом замены элементов яв­ляется факт использования замены элемента для получения информации о его состоянии.

Для нахождения оптимальной процедуры восстановления работо­способности должен быть задан критерий оптимальности. Таких критериев известно, по крайней мере, три: средняя стоимость восстановления работо­способности, вероятность восстановления работоспособности с ограни­ченной стоимостью, стоимость устранения отказов с заданной вероятно­стью. Эти критерии отражают различные практические условия. Так, при необходимости оптимизации многократного восстановления работоспо­собности наиболее естественна в качестве критерия средняя стоимость. Нетрудно указать ситуации, когда в качестве критериев задаются послед­ние два, особенно если под стоимостью подразумевается время восстанов­ления работоспособности.

Для решения задачи необходимы также некоторые дополнительные сведения об объекте (например, условные распределения вероятностей от­казов элементов, если отказы зависимы) или ограничения, накладываемые на процедуру (например, порядок замен элементов).

Будем считать, что если проверка охватывает некоторую совокуп­ность элементов, то по ее результатам можно судить лишь о состоянии данной совокупности элементов. О состоянии других элементов можно су­дить только по методу исключения.

Если информация, полученная в результате проведения проверки, свидетельствует об отказе хотя бы одного из проверенных элементов, бу­дем говорить об отрицательном результате проверки. В противном случае результат проверки назовем положительным. Таким образом, каждая про­верка разделяет все множество возможных состояний системы на два не­пустых подмножества, соответствующие положительному и отрицатель­ному результатам проверки.

Весьма важными являются сведения о достоверности проверок. Ко­личественной мерой достоверности проверок можно считать вероятности ошибок двух родов, возникающих по ряду причин. К этим причинам можно отнести следующие:

а) погрешности измерительных и контрольных приборов, погрешно­сти формирования контрольных сигналов, помехи в каналах связи и т.п.;

б) отказы в диагностической системе;

в) отказы в объекте диагностики, имеющие перемежающийся харак­тер, а также несовпадение времени проведения проверки со временем по­явления отказа в объекте.

Заметим, то перемежающиеся отказы в объекте диагностики могут быть причиной лишь ошибок первого рода – «пропуска» отказавших эле­ментов. Остальные перечисленные причины могут вызвать как «пропуск» отказов, так и «ложные тревоги» – принятие работоспособных элементов за неработоспособные.

Таким образом, мы кратко рассмотрели различные процедуры по­иска и локализации дефектов, приводящие к восстановлению работоспо­собности сложной системы.

В заключение отметим, что в последних разделах этой главы основ­ное внимание будет уделено вероятностным процедурам локализации де­фектов в сложных гибридных системах с использованием аппарата экс­пертных систем и нечетких множеств, как наиболее слабо освещенных в учебно-методической литературе.