Модель роста надежности

Вероятно, самой известной моделью надежности является модель, разработанная Джелински и Морандой [7] и Шуманом [8]. Она опирается на теорию надежности аппаратуры, основы которой были приведены в подразд. 1.2. В частности, в данной модели используются: вероятность безотказной работы P (t), интенсивность отказов λ(t) и среднее время ме­жду отказами Т.

Один из способов оценки среднего времени между отказами – на­блюдение за поведением программы в течение некоторого периода вре­мени и нанесение на график значений времени между последовательными ошибками. Можно надеяться, что при этом будет обнаружено явление роста надежности;помере того как ошибки обнаруживаются и исправ­ляются, время между последовательными ошибками становится больше. Экстраполируя эту кривую в будущее, можно предсказать среднее время между отказами в любой момент времени и предсказать полное число ошибок в программе.

Такая экстраполяция, однако, в слишком большой степени основана на догадках и обычно уводит в сторону. Было бы лучше опираться на ка­кое-то априорное представление об имеющемся распределении вероятно­стей ошибок, затем исполь­зовать сведения о найденных ошибках для оценки параметров этого распределения и только потом использовать эту модель для пред­сказания событий в будущем.

Разработка такой модели начинается с уточнения поведения функ­ции λ(t)– интенсивности отказов ПО.В большинстве моделей аппаратного обеспечения λ(t) сначала уменьшается со временем (этап, когда обнаружи­ваются и исправляются ошибки проектирования и производства), затем ос­тается постоянной в течение большей части срока службы системы (соот­ветствует случайным отказам) и в конце полезного срока службы системы увеличивается (см. рис. 3.1). В теории надежности аппаратуры в ос­новном рассматривается средний пе­риод, где интенсивность отказов по­стоянна. Однако предположение о постоянстве интенсивности отказов вряд ли при­менимо в случае программного обеспечения, для которого эта функция должна уменьшаться по мере обнаружения и исправления оши­бок. По­этому, как показано на рис. 3.6, интенсивность отказов со временем уменьшается.

Рис. 3.6. Предполагаемая интенсивность отказов

Первое существенное предположение состоит в том, что λ(t)посто­янно до обнаружения и исправления ошиб­ки, после чего λ(t)опять стано­вится константой, но уже с другим, меньшим, значением. Это означает, что λ(t)пропорционально числу оставшихся ошибок. Второе предположение состоит в том, что λ(t) прямо пропорционально числу оставшихся ошибок, т.е.

λ(t) = – K (N – i), (3.1)

где N – неизвестное первоначальное число ошибок; i – число обнаружен­ных ошибок; K – некоторая неизвестная константа. Каждый раз, когда ошибка обнаруживается (модель предполагает, что задержка между обна­ружением ошибки и ее исправлением отсутствует), λ(t)уменьшается на не­которую величину K. На оси времени может быть представлено календар­ное время или время работы программы (последнее может быть масштаби­ровано с учетом интенсивности ис­пользования программы).

Параметры N и K можно оценить, если некоторое количество оши­бок уже обнаружено (например, если фаза тестирования уже частично пройдена). Предположим, что обнаружено п ошибок, а х:[1], х [2],..., х [ n ]– интервалы времени между этими ошибками. В предположении, что λ(t)по­стоянно между ошибками, плотность вероятности для x [ i ]

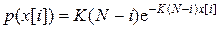. (3.2)

Полагая Т равным сумме х -ов и используя функцию максималь­ного правдоподобия для этого уравнения, получаем второе уравнение:

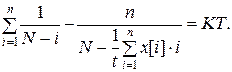(3.3)

K и N в этих уравнениях – приближения для рассмотренных выше K и N. Получилось два уравнения с двумя неизвестными N и K. Зная, что обнару­жено п ошибок с интервалами x [ i ]между ними, эти уравнения можно ре­шить относительно N и K с помощью простой программы численного ана­лиза. Значение N дает основной результат – оценку полного числа ошибок. Знание параметра K позволяет использовать уравнения для предсказания времени до появления (n +1)-й ошибки, (n +2)-й и т.д.

Эта основная модель может быть развита в различных направ­лениях. Например, частота отказов нередко увеличивается после завершения неко­торого начального периода, по мере того как раз­рабатываются тесты или программа начинает использоваться ин­тенсивнее.

Чтобы очертить границы применимости этой модели, тре­буется по­нимать лежащие в ее основе допущения (упрощения).

Первое из них – ошибка исправляется немедленно (или программа не используется до тех пор, пока найденная ошибка не будет исправлена). Предполагается также, что программа не изменяется (за исключением ис­правления ошибок). Второе допущение – при всех исправлениях найден­ные ошибки устра­няются, и новых ошибок не вносится.

Третье, основное, допущение – это то, что функция λ(t) носит одина­ковый характер для всех программ. Тем самым предполагается, что каждая ошибка уменьшает λ(t)на постоянную величину K – на практике это, веро­ятно, нереально, однако, по-видимому, с такого предположения вполне ра­зумно начать. Хотя желание выразить надежность программного обеспе­чения некото­рой функцией времени вполне разумно, следует понимать, что в действительности она от времени не зависит. Надежность программ­ного обеспечения является функцией числа ошибок, их серьез­ности и их расположения, а также того, как система используется.

В реальности частота отказов в большой системе при измерении в течение нескольких лет может иметь тенденцию к по­нижению, но внутри этого периода возможны большие колебания. Анализ частоты обнаруже­ния ошибок при тестировании 14 различ­ных систем [1] показал, что час­тота эта в пяти проектах достигала пика в начале работы, в пяти – в сере­дине и в четырех – в конце.

Отметим, наконец, что описанная выше модель ка­жется чересчур оп­тимистичной. Например, при п = 10 (десять обна­руженных ошибок) с ин­тервалами между отказами (в минутах)

9, 17, 21, 54, 32, 78, 82, 33, 57, 82

модель предсказывает, что осталось 3,3 ошибки (т.е. изначально в про­грамме было N = 13,3 ошибки). При этом интер­валы времени между 10, 11, 12 и 13 ошибками оцениваются в 135, 245 и 1265 минут.