Модель совершенно другого типа разработал Миллс [13]. В ней не используется никаких предположений о поведении интенсивности отказов λ(t), эта модель строится на твердом статистическом фундаменте. Сначала программа «засоряется» некоторым количеством известных ошибок. Эти ошибки вносятся в программу случайным образом, а затем делается предположение, что для исходных и внесенных в программу ошибок вероятность обнаружения при последующем тестировании одинакова и зависит только от их количества. Тестируя программу в течение некоторого времени и сравнивая количество обнаруженных исходных и внесенных в программу ошибок, можно оценить N – первоначальное число ошибок в программе.
Предположим, что в программу было внесено s ошибок, после чего решено начать тестирование. Пусть при тестировании обнаружено n+v ошибок, причем п – число найденных исходных ошибок, a v – число найденных внесенных ошибок. Тогда оценка для N по методу максимального правдоподобия будет следующей:
 (3.4)
(3.4)
Например, если в программу внесено 20 ошибок и к некоторому моменту тестирования обнаружено 15 исходных и 5 внесенных ошибок, значение N можно оценить в 60. В действительности N можно оценивать после обнаружения каждой ошибки; Миллс [13] предлагает во время всего периода тестирования отмечать на графике число найденных ошибок и текущие оценки для N.
Вторая часть модели связана с выдвижением и проверкой гипотез об N. Примем, что в программе имеется не более k исходных ошибок, и внесем в нее еще s ошибок. Теперь программа тестируется, пока не будут обнаружены все внесенные ошибки, причем в этот момент подсчитывается число обнаруженных исходных ошибок (обозначим его п).Уровень значимости С вычисляется по следующей формуле:
 (3.5)
(3.5)
Величина С является мерой доверия к модели; это вероятность того, что число исходных ошибок будет не больше k. Например, если мы утверждаем, что в программе нет ошибок (k = 0), и, внеся в программу 4 ошибки, все их обнаруживаем, не встретив ни одной исходной ошибки, то С = 0,80. Чтобы достичь уровня 95 %, нам надо было бы внести в программу 19 ошибок. Если мы утверждаем, что в программе не более трех исходных ошибок, и, внеся шесть ошибок, обнаруживаем их все и не более трех исходных, уровень значимости равен 60 %. Формула для С имеет под собой прочные статистические основания; выведена она Миллсом [13].
Эти две формулы для N и С образуют полезную модель ошибок; первая предсказывает число ошибок, а вторая может использоваться для установления доверительного уровня прогноза. Слабость этой формулы в том, что С нельзя предсказать до тех пор, пока не будут обнаружены все внесенные ошибки (а это, конечно, может не произойти до самого конца этапа тестирования). Чтобы справиться с этой трудностью, можно модифицировать формулу для С так, чтобы С можно было оценить после того, как найдено j внесенных ошибок (j £ s)[14]:
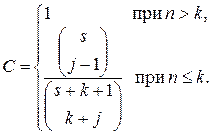 (3.6)
(3.6)
В предыдущем примере, где k = 3, a s = 6, если найдены 5 из 6 внесенных ошибок, С опускается с 60 до 33 %. Еще один график, который полезно строить во время тестирования, – текущее значение верхней границы k для некоторого фиксированного доверительного уровня, например 90 %.
Модель Миллса одновременно математически проста и интуитивно понятна. Легко представить себе программу внесения ошибок, которая случайным образом выбирает модуль, вносит логическую ошибку, изменяя или убирая операторы, и затем заново его компилирует. Природа внесенной ошибки должна сохраняться в тайне, но все их следует регистрировать, чтобы впоследствии можно было разделять ошибки на исходные и внесенные.
Процесс внесения ошибок в настоящее время является самым слабым местом модели, поскольку предполагается, что для исходных и внесенных ошибок вероятность обнаружения одинакова (но неизвестна). Из этого следует, что внесенные ошибки должны быть «типичными» образцами ошибок, но мы еще недостаточно хорошо понимаем программирование, чтобы сказать, какими именно должны быть типичные ошибки. Однако по сравнению с проблемами, стоящими перед другими моделями надежности, эта проблема кажется относительно несложной и вполне разрешимой.
Наконец, отметим еще одно достоинство внесения ошибок: оно может оказывать положительное психологическое влияние на группу тестирования. У программистов возникают затруднения при отладке своих программ, например, потому, что они склонны считать каждую обнаруженную ошибку последней. Внесение ошибок может помочь в этом деле, поскольку теперь программист знает, что в его программе есть еще не обнаруженные ошибки.






