Входной величиной измерительного прибора является его измеряемая величина. Наибольшее и наименьшее значения измеряемой величины, для которых нормированы погрешности, называются пределами измерения. Область значений, заключенная между верхним и нижним пределами измерения, называется диапазоном измерений. От диапазона измерений следует отличать диапазон показаний, который охватывает область значений шкалы, ограниченную конечным и начальным значениями шкалы. Таким образом, диапазон измерений, охватывающий часть шкалы, в пределах которой измерения могут быть проведены с нормируемой погрешностью, более узок, чем диапазон показаний, охватывающий всю шкалу.
Выходной величиной измерительного прибора является изменение состояния отсчетного устройства, например положения стрелки стрелочного прибора.
Функция (уравнение) преобразования— функциональная зависимость между выходной величиной у и входной величиной х. Как и любая функция, функция преобразования может задаваться аналитически (уравнением), таблично или графически. В аналитическую функцию преобразования обычно входят конструктивные параметры прибора или преобразователя и поэтому она используется при расчете и проектировании. Функция преобразования реального преобразователя определяется экспериментально. В ходе опыта определяется зависимость вы ходной величины от входной. Для упрощения анализа полученной функции по табличным данным строится график.
Обычно желательно, чтобы функция преобразования была линейной.
Чувствительность— это отношение изменения выходной величины измерительного прибора или измерительного преобразователя к вызвавшему ее изменению входной величины. Чувствительность определяется выражением
(1.14)
и может быть определена при любом способе задания функции преобразования.
В важном частном случае, когда выходная величина изменяется пропорционально входной, S =у/х, где у— значение выходной величины, соответствующее входной величине х. При нелинейной функции преобразования чувствительность зависит от значения входной величины.
Для прибора или преобразователя может определяться абсолютная, относительная и приведенная погрешности.
Абсолютная погрешность прибора в данной точке диапазона измерения равна
(1.15)
где х П—показание прибора; х— истинное значение измеряемой величины. Однако в связи с тем, что истинное значение неизвестно, на практике вместо него используется действительное значение х Д. В качестве х Дпринимают показания более точного, образцового прибора. Абсолютная погрешность прибора выражается в тех же единицах, что и измеряемая величина.
Относительная погрешность прибора равна отношению абсолютной погрешности к истинному значению измеряемой величины и обычно выражается в процентах:
(1.16)
Приведенная погрешность прибора g также выражается в процентах и равна отношению абсолютной погрешности к нормирующему значению х N, которое принимается равным верхнему пределу измерений (если нулевая отметка находится на краю или вне шкалы) или диапазону измерения (если нулевая отметка находится внутри диапазона измерений), %:
(1.17)
Значения абсолютной, относительной и приведенной погрешностей используются для нормирования погрешности приборов.
Абсолютную погрешность измерительного преобразователя невозможно определить по выражению (1.15), поскольку входная и выходная величины могут иметь различную физическую природу, а также вследствие того что часто отсутствует образцовый измерительный преобразователь, по которому можно было бы проверить рабочий преобразователь. Различают номинальную функцию преобразования измерительного преобразователя у ном =f ном (х) которую он должен иметь согласно государственным стандартам, техническим условиям или другим нормативным документам, и реальную у= f (х), которую он имеет в действительности. Разность значений действительной и номинальной функций преобразования при одном и том же значении входной величины определяет абсолютную погрешность преобразователя по выходу:
(1.18)
Погрешность создается преобразователем. Однако часто бывает полезно знать значение входного сигнала, соответствующего погрешности преобразователя. Абсолютным значением погрешности преобразователя по входу называется разность
(1.19)
где х— истинное значение входной величины; x ном—значение входной величины, определяемое по номинальной функции преобразования у ном =f ном (х), при значении выходной величины у ном, соответствующей истинному значению х.
Относительные погрешности по выходу и входу определяются соответственно равенствами
(1.20)
и
(1.21)
Приведенные погрешности по выходу и входу
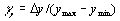(1.22)
и
(1.23)
где х maxи у max — максимальные значения входной и выходной величин, а x min и у min — их минимальные значения.
Очевидно, при пропорциональной функции преобразования у= S(x) значения относительных погрешностей так же как и приведенных погрешностей по входу и выходу совпадают.
В технике часто используются преобразователи с линейной функцией преобразования
(1.24)
где S —чувствительность преобразователя; y 0 — значение выходной величины при нулевом значении входной.
Отклонение такой функции преобразования от номинальной может быть вызвано отклонением y 0 и отклонением чувствительности S. Погрешность, обусловленная неноминальным значением выходной величины при нулевом значении
входной y 0, называется аддитивной. Погрешность, обусловленная неноминальным значением чувствительности S, называется мультипликативной.
Аддитивная погрешность не зависит от входной величины. При изменении y 0вследствие каких-либо причин график функции преобразования перемещается параллельно самому себе (рис. 1.2). Значение этой погрешности
(1.25)
где у 0 ном — номинальное значение у 0.
При мультипликативной погрешности наклон прямой, графически отображающий функцию преобразования, отличается от наклона при номинальной функции преобразования (рис. 1.3). При этом абсолютная погрешность D у=у—у 0зависит от входной величины х.
Действительно, пусть чувствительность изменилась на D S и стала равной S = S ном +D S, где S ном—номинальное ее значение. В этом случае абсолютная погрешность преобразователя
(1.26)
т.е. абсолютная мультипликативная погрешность пропорциональна входной величине х.
Рассмотрим относительную мультипликативную Погрешность при пропорциональной функции преобразования у= S ном (x):
(1.27)
Относительная мультипликативная погрешность равна относительному изменению чувствительности.
Погрешность измерительных средств зависит от условий проведения измерений. При этом различают основную и дополнительные погрешности. Основной погрешностью называется погрешность, существующая при так называемых нормальных условиях, которые указаны в нормативных документах, регламентирующих правила испытания и эксплуатации данного средства измерения. Например, под нормальными условиями могут пониматься: температура окружающей среды (+20± 2)° С; положение прибора горизонтальное с отклонением от горизонтального, не превышающем ± 2° С; относительная влажность (65± 15)%, практическое отсутствие магнитных и электрических полей; частота питающей сети (50± 1) Гц и т.д.
Дополнительная погрешность возникает при отклонении условий испытания и эксплуатации средства измерения от нормальных. Она нормируется значением погрешности, вызванной отклонением одной из влияющих величин от ее нормального значения или выходом ее за пределы нормальной области значений. Например, приведенная погрешность прибора при нормальных условиях, т.е. в диапазоне температур (+20± 2)° С, не превышает 1 %. Если температура лежит вне указанного диапазона, то погрешность может быть больше указанной. Например, приведенная дополнительная погрешность при изменении температуры на 10° С не должна превышать 1%.
Нормирование погрешности средств измерения производится по максимально допускаемым значениям основной и дополнительной погрешностей (ГОСТ8.401-80). Погрешность средств измерения не должна превышать одного из перечисленных ниже пределов.
а) Если погрешность имеет аддитивный характер, то предел допускаемой абсолютной погрешности не должен превышать
(1.28)
б) Если погрешность имеет как аддитивную, так и мультипликативную составляющую, то предел допускаемой абсолютной погрешности не должен превышать
(1.29)
в) Если погрешность имеет мультипликативный характер, то предел допускаемой относительной погрешности не должен превышать
(1.30)
г) Если погрешность имеет как аддитивную, так и мультипликативную составляющие, то предел допускаемой относительной погрешности (в процентах) не должен превышать
(1.31)
где a, b,c и d— постоянные; x к—конечное значение диапазона измерения. Из (1.31) следует, что при х =0 предел абсолютной погрешности
(1.32)
апри x = x к
(1.33)
д) Приведенная погрешность не должна превышать значения
(1.34)
При нормировании погрешности средства измерения постоянные а, b, с, d выбираются из следующего ряда чисел:
1 10n;1,5 10n;2 10n; 2,5 10n; 4 10n; 5 10n; 6 10n,
где n= 1; 0; -1; - 2 и т.д.
Средствам измерения присваивается класс точности. Это обобщенная метрологическая характеристика, определяемая пределами допускаемых основной и дополнительных погрешностей, значения которых устанавливаются в стандартах на отдельные виды средств измерения. Класс точности обозначается числом, соответствующим нормированной основной погрешности средства измерения. Для случая (r) класс точности обозначается в виде дроби с/ d например: 0,1 /0,05.
Класс точности стрелочных и самопишущих приборов, как правило, обозначается одним числом, равным максимально допускаемому значению основной приведенной погрешности с, тогда как класс точности цифровых приборов, мостов и компенсаторов указывается в виде дроби с/ d.
Конкретные ряды классов точности устанавливаются в стандартах на отдельные виды средств измерения.
Отдельными характеристиками погрешности являются вариации показаний прибора и порог чувствительности. Вариация показаний прибора—это наибольшая разность его показаний при одном и том же значении измеряемой величины. Основной ее причиной является трение в опорах подвижной части прибора. Вариацию определяют, сравнивая показания прибора, считанные один раз после установки требуемого значения измеряемой величины подходом снизу (со стороны меньших значений), а другой раз—подходом сверху (со стороны больших значений).
Порог чувствительности—это изменение измеряемой величины, вызывающее наименьшее изменение показаний, различимое при нормальном для данного прибора способе отсчета.
Собственное потребление мощности прибором из цепи, в которой производится измерение, является важной характеристикой прибора. Оно приводит к изменению электрических параметров этой цепи и отрицательно влияет на точность измерения. Особенно сильно это проявляется при измерениях в маломощных цепях. В зависимости от устройства, конструкции и назначения прибора потребляемая им мощность может колебаться от 1 0-12 Вт до нескольких ватт.
Динамические характеристики. Описанные выше характеристики являются статическими, т.е. не зависящими от времени. Они, строго говоря, имеют смысл только в том случае, если параметры измерительного прибора (или другого средства измерения) и значение измеряемой величины остаются постоянными, а время измерения не ограничено. На практике, однако, эти условия часто не соблюдаются: измеряемая величина меняется по времени, измерение обычно нужно проводить за возможно более короткое время, параметры измерительного прибора только приближенно можно считать неизменными. Одновременный учет всех этих особенностей процесса измерения затруднителен. Имеется, однако, много случаев, когда о законе изменения входной величины за время измерения могут быть высказаны достаточно обоснованные предположения и когда средство измерения является линейной системой, т.е. может быть характеризовано линейным дифференциальным уравнением с постоянными коэффициентами:
(1.35)
где а 0, а 1 ,...,a n — постоянные коэффициенты.
Нередко можно считать, что до момента времени t =0 входная величина была постоянной и начала изменяться лишь при t =0. Если при этом отсчитывать значения входной величины от значения, которое она имела до t =0, то получим нулевые начальные условия. Такое рассмотрение упрощает определение реакции звена у(t) на изменение входной величины. При нулевых начальных условиях уравнение (1.35) в операторной форме имеет вид
(1.36)
где р = p/dt— оператор.
Передаточной функцией преобразователя называется отношение изображений по Лапласу выходной величины к входной:
(1.37)
Зная передаточную функцию преобразователя, можно определить его реакцию у(t) на заданное изменение измеряемой величины х(t) и определить динамическую погрешность
(1.38)
где у(t)— значение выходной величины измерительного средства в момент времени t; у ст — значение выходной величины, заданное его статической функцией преобразования.
При анализе динамических характеристик используются следующие типовые входные воздействия.
- Единичная функция. При таком воздействии входная величина равна 0 при t < 0 и единице при t? 0. При единичной функции переходной процесс преобразователя определяется соотношением
(1.39)
где L-1 —символ обратного преобразования Лапласа.
2. Гармоническая функция. При гармоническом изменении входной величины 
, где Х m — амплитуда ее изменения; w —ее круговая частота, выходная величина изменяется также гармонически: 
где У m —амплитуда выходной величины. Отношение реакции преобразователя ко входному воздействию определяет частотную передаточную функцию (комплексную чувствительность
(1.40)
где А(w) —модуль частотной передаточной функции; j (w) —сдвиг фаз между входной и выходной величинами.
Связь между частотной передаточной функцией и передаточной функцией выражается соотношением
при p = jw. (1.41)
Зависимость модуля частотной передаточной функции от частоты А(w) определяет амплитудно-частотную характеристику преобразователя; зависимость ее аргумента от частоты j (w) определяет фазочастотную характеристику.
К важным динамическим характеристикам приборов относится время установления показаний— промежуток времени, прошедший с момента подключения или изменения измеряемой величины до момента, когда отклонение указателя от установившегося значения не превышает 1,5% длинны шкалы. Для многих приборов это время не превышает 4с. Временем установления показаний характеризуются показывающие приборы, имеющие указатель и шкалу. Для цифровых приборов указывается время измерения, отсчитываемое от начала измерения или изменения измеряемой величины, до получения результата на отсчетном устройстве с нормированной погрешностью.
Обычно стремятся иметь приборы, обеспечивающие малые времена установления показаний (в случае цифровых приборов—малые времена измерения).
Надежность прибора—способность сохранять заданные характеристики при определенных условиях в течение заданного времени. Выход значения параметров и характеристик прибора за пределы нормы считается отказом. Отказ измерительного прибора может наступить, если его действительная погрешность станет больше ее нормирующего значения, определяемого классом точности.
Количественным показателем надежности является наработка на отказ— среднее время безотказной работы прибора. Наработка на отказ является статистической величиной. Она устанавливается для данной серии приборов на основании выборочных испытаний небольшой их партии, входящих в эту серию.
Согласно ГОСТ 22261—82 приборы характеризуются также их механической и электрической прочностью, сопротивлением изоляции и некоторыми другими параметрами.
