Адекватным математическим аппаратом описания случайных погрешностей является теория вероятностей. Согласно последней случайная величина наиболее полно характеризуется своим законом распределения (или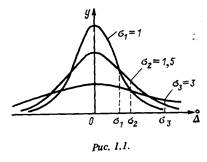 
плотностью распределения) вероятностей. Измерителям чаще всего приходится принимать нормальную и равномерную плотность распределения. Возможны и другие законы распределения, которые обычно аппроксимируются стандартными функциями. Если выполняются предположения о том, что погрешности измерений могут принимать непрерывный ряд значений, при большом числе измерений частота появления погрешностей, равных по абсолютной величине, но различного знака, одинакова и малые погрешности встречаются чаще, чем большие, то тогда для описания случайных погрешностей следует применять нормальный закон распределения вероятностей, для которого
(1.4)
где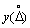 
— плотность вероятностей случайной погрешности 
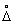; s — среднее квадратическое значение случайной погрешности.
Кривые, соответствующие выражению (1.4) для разных значений s, приведены на рис. 1.1. Видно, что при малых значениях о вероятней получить малую погрешность измерений, нежели при больших.
Вероятность того, что погрешность результата измерения находится между заданными предельными значениям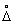и 1, и 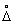2 , вычисляется по формуле
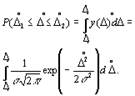(1.5)
Интеграл в формуле (1.5) можно вычислить, используя таблицы функции Лапласа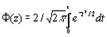 
, приводимые в книгах по теории вероятностей и статистической обработке экспериментальных результатов [2,28]. Нетрудно заметить, что
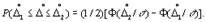(1.6)
В табл. 1.1 приведены значения вероятностей для некоторых интервалов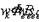 
, заданных в единицах s.
Таблица 1.1
Интервал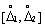 
| Вероятность 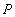 Попадания в интервал 
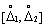
| 1- P |
| 0,5 | 0,5 |
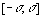
| 0,68 | 0,32 |
| 0,95 | 0,05 |
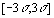
| 0,997 | 0,003 |
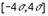
| 0,99993 | 0,00007 |
В первом столбце табл. 1.1 указываются интервалы, характеризуемые своими нижними и верхними границам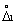и 
и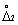 
соответственно. Второй столбец дает вероятности P того, что случайная погрешность результата измерения не выходит за границы соответствующих интервалов. В третьем столбце показано, каковы вероятности выхода случайной погрешности за пределы интервалов.
Согласно табл. 1.1 вероятности получения значения случайных погрешностей в интервале [-2/3s ,2/3s ] и за его пределами одинаковы, в то время как в среднем только 0,3%измерений имеют погрешности, абсолютное значение которых превышает 3s. Значение погрешности 2/3s называется вероятной погрешностью, а значение 3s часто считают практически наибольшей возможной погрешностью. Однако при большом числе измерений (n >20 30) максимальная погрешность нередко может превышать 3.
Как уже указывалось, часто распределение погрешностей можно принять равномерным:
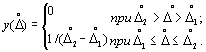
Такой закон распределения характерен, например, для погрешностей отсчета по шкале прибора, погрешностей дискретности в цифровых измерительных приборах, погрешностей квантования в аналого-цифровых преобразователях (АЦП).
Рассмотрим далее оценки параметров распределения случайных погрешностей прямых измерений. Напомним, что случайная абсолютная погрешность определяется формулой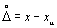 
, где x — результат измерения; x и — истинное значение измеряемой величины. Если было проведено n прямых измерений одной и той же величины, то в общем случае в каждом из актов измерений погрешность будет разной: 
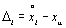, где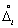 
— погрешность i -го измерения; x i— результат i- го измерения.
Поскольку истинное значение измеряемой величины x и неизвестно, непосредственно случайную абсолютную погрешность вычислить нельзя. При практических расчетах приходится вместо x и использовать его оценку. Обычно принимают, что истинное значение равно среднему арифметическому значению ряда измерений:
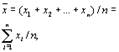(1.7)
где x i— результаты отдельных измерений; n— число измерений.
Теперь аналогично 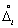можно определить отклонение результата каждого измерения от среднего значения 
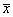как
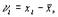(1.8)
а затем по формуле
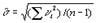(1.9)
вычислить оценку 
значения среднеквадратической погрешности данного ряда измерений. Согласно теории вероятностей при достаточно большом числе измерений, имеющих независимые случайные погрешности, оценка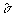 
сходится по вероятности к s. Таким образом,
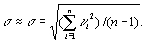(1.10)
Ввиду того что среднее арифметическое значение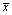 
также является случайной величиной, имеет смысл понятие среднеквадратического отклонения среднего арифметического значения 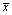. Эту величину обозначим символом 
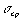. Можно показать, что для независимых погрешностей
(1.11)
Значение s ср характеризует степень разброса 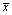. Как указывалось выше, 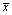выступает оценкой истинного значения измеряемой величины, т.е. является конечным результатом выполняемых измерений. Поэтому s ср называют также средней квадратической погрешностью результата измерений.
На практике значением s, вычисляемым по (1.10), пользуются в том случае, если необходимо дать характеристику точности применяемого метода измерения: если метод точен, то разброс результатов отдельных измерений мал, т.е. мало значение s Значение же s ср вычисляемое по (1.11), используется для характеристики точности результата измерений некоторой величины, т.е. результата, полученного посредством математической обработки итогов целого ряда отдельных прямых измерений.
Введем важные понятия доверительной вероятности и доверительного интервала. Как указывалось выше, среднее арифметическое значение 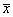, полученное в результате некоторого ряда измерений, является оценкой истинного значения x и и, конечно, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть P Д есть вероятность того, что 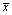отличается от x и не более чем на D, т.е.
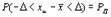
или
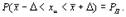
Вероятность P Д называется доверительной вероятностью, а интервал значений измеряемой величины от 
до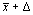 
— доверительным интервалом.
Приведенные выше неравенства означают, что с вероятностью P Д доверительный интервал от до 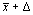заключает в себе истинное значение x и Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами — доверительной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал. В частности, при достаточно большом числе измерений часто бывает оправданным использование нормального закона, в то время как при небольшом числе измерений (n<20), результаты которых принадлежат нормальному распределению, следует пользоваться распределением Стьюдента. Это распределение имеет плотность вероятностей, практически совпадающую с нормальной при больших n, но значительно отличающуюся от нормальной при малых n.
В табл. 1.2 приведены так называемые квантили распределения Стьюдента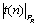 
для числа измерений n=2? 30 и доверительных вероятностей P Д =0,8? 0,99. Более полную таблицу можно найти, например, в [2]. Укажем, однако, что обычно таблицы распределения Стьюдента приводятся не для значений n и 
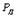, а для значений m=n- 1 и a =1- P Д, что следует учитывать при пользовании ими. Чтобы определить доверительный интервал, надо для данных n и P Д найти квантиль 
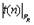и вычислить величины
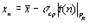и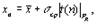 
Ттаблица 1.2. Квантили распределения Стьюдента
| Число измерений N | Доверительная вероятность P Д | ||||||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |||||
| 3,08 1,89 1,64 1,53 1,48 1,44 1,42 1,40 1,38 1,37 1,36 1,36 1,35 1,34 1,34 1,33 1,31 | 6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,84 1,81 1,80 1,78 1,77 1,76 1,75 1,73 1,70 | 12,7 4,30 3,18 2,77 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 2,14 2,12 2,09 2,04 | 31,8 6,96 4,54 3,75 3,36 3,14 3,00 2,90 2,82 2,76 2,72 2,68 2,65 2,62 2,58 2,54 2,47 | 63,7 9,92 5,84 4,60 4,03 3,71 3,50 3,35 3,25 3,17 3,11 3,05 3,01 2,98 2,92 2,87 2,76 | |||||
которые будут являться верхней и нижней границами доверительного интервала.
Примеры нахождения доверительных интервалов для заданной доверительной вероятности приведены ниже. Там же показана одна из наиболее употребительных форм записи результата измерения в виде
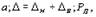
где a — результат измерения в единицах измеряемой величины; D — погрешность измерения; D В и D Н — верхняя и нижняя границы погрешности измерения; P Д — доверительная вероятность.
Пример 1. Произведено 17 отсчетов значений измеряемой величины — напряжения (см. ниже). Требуется произвести обработку результатов измерений (предполагая их нормальное распределение). Для этого выбрать доверительную вероятность P Д =0.95. Систематической погрешностью пренебречь.
| 
|
|
|
|
|
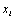
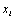
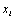
— номер измерения, x i— результат измерения.
Обработку результатов измерений будем вести в следующей последовательности.
1. Определим среднее арифметическое значение результатов отдельных измерений по формуле (1.7):
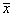= (1681 + 1701 + 1693 + 1678 + 1686 + 1674 + 1705 + 1685 + 1697 + + 1690 + 1690 + 1685 + 1682 + 1690 + 1687 + 1680 + 1692) /17 =
= 1688,0 мВ.
Значение 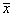будем считать оценкой истинного значения измеряемого напряжения U, т.е. U = 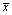@ 1688,0 мВ.
2. Вычислим отклонения результатов отдельных измерений от среднего значения 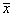по формуле (1.8):
|
| 
|
|
|
|
|
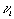
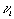
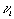
| -7 –10 –2 –14 | –3 –3 | –6 –1 –8 |
3. Вычислим оценку 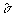значения средней квадратической погрешности ряда измерений по формуле (1.9):
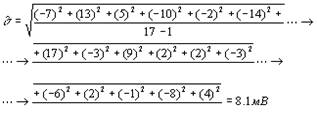
Согласно (1.10)
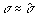=8,1 мВ.
Далее по (1.11) определим
s ср = 8,1/? 17» 2,0 мВ.
Для вычисления доверительного интервала, соответствующего доверительной вероятности P Д = 0,95 и числу измерений n= 17, следует воспользоваться табл. 1.2.
Находим значение квантиля:
Поскольку s ср = 2мВ, то нижняя граница доверительного интервала
а верхняя граница
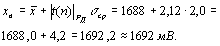
Нижняя и верхняя границы погрешности измерения
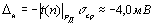
и
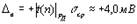
соответственно.
Результат измерения может быть записан в виде
U= 1688мВ; D =+4мВ; Р Д = 0,95.
Пример 2. Произведено 10 отсчетов значений измеряемой величины—напряжения (см. ниже). Задание то же, что и в примере 1.
|
|
|
|
| 
|
|
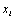
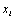
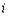
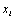
Следуя той же последовательности действий что и в примере 1, получим
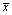= 1689,0мВ, т.е. U 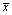= 1689,0мВ;
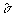» 10мВ, т.е. 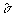= 10мВ;
s ср=3,2мВ.
Находим из табл.1.2 значение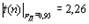 
. Следовательно, границы доверительного интервала
x н = 1689,0-2,26? 3,2=1681,8=1682мВ;
x в = 1689,0+2,26? 3,2=1696,2=1696мВ.
Результат измерения записывается в виде
U = 1689мВ; D =± 7 мВ; P Д =0,95.
Сравнение результатов измерения в примерах 1 и 2 показывает, что при уменьшении числа измерений с 17 до 10 происходит увеличение доверительного интервала, соответствующего одной и той же доверительной вероятности P Д = 0,95.
Случайные погрешности косвенных измерений. Если величина А является функцией величин Х, У,..., Z [А= f (Х, У,..., Z ]и определяется на основании прямых измерений этих величин, то средняя квадратическая погрешность измерения величины А может быть вычислена по формуле
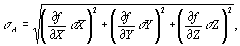(1.12)
где s X, s Y,…, s Z — средние квадратические погрешности измерения величин Х, У,..., Z соответственно.
Производные вычисляются в точке (Х, У,..., Z). Формула (1.12) справедлива в том случае, если величины Х, У,..., Z независимы (или некоррелированы).
Суммирование погрешностей. При измерениях может быть несколько источников как систематических, так и случайных погрешностей. Поэтому практически важным является вопрос о правилах нахождения суммарной погрешности измерения по известным значениям погрешностей составляющих ее частей. При суммировании составляющих неисключенной систематической погрешности их конкретные реализации можно рассматривать как реализации случайной величины. Если известны границы i составляющих неисключенной систематической погрешности, а распределение этих составляющих в пределах границ равномерно, то граница неисключенной систематической погрешности результата измерения вычисляется по формуле
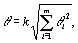
где k —коэффициент, определяемый принятой доверительной вероятностью. При доверительной вероятности 0,95 он принимается равным 1,1 (ГОСТ 8.207-76).
При суммировании случайных погрешностей необходимо учитывать их корреляционные связи. Суммарная средняя квадратическая погрешность при двух составляющих может быть вычислена по формуле
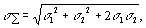(1.13)
где s 1, и s 2 —средние квадратические погрешности отдельных составляющих; r — коэффициент корреляции.
Поскольку на практике трудно получить удовлетворительную оценку коэффициента r, приходится ограничиваться крайними случаями, т.е. считать, что либо r = 0, либо r =± 1. Тогда приведенная выше формула примет вид
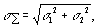если r = 0
или
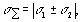если r =± 1.
Таким образом, при отсутствии корреляционной связи средние квадратические погрешности складываются геометрически, а в случае жесткой корреляционной зависимости—алгебраически. Этот вывод справедлив и для случая нескольких источников погрешностей.
Правила нахождения границы погрешности результата измерения при одновременном наличии как неисключенных систематических, так и случайных погрешностей также регламентируются ГОСТ 8.207-76 и заключаются в следующем. Если q /s? < 0,8, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата
где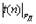 
—коэффициент Стьюдента, определяемый по табл. 1.2. Если q /s? > 8, то, наоборот, пренебрегают случайной погрешностью по сравнению с систематической и считают, что граница погрешности результата D? =q.
В случае, если эти неравенства не выполняются, следует найти композицию распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины, вычислить значение среднего квадратического отклонения и затем границы суммарной погрешности результата измерения. Допускается также определение границы погрешности результата измерения при помощи приведенных в ГОСТ 8.207-76 эмпирических формул.
Исключение грубых погрешностей. Выделение грубых погрешностей (промахов) не простая задача, она требует достаточно глубокого понимания особенностей поведения измеряемой величины. Наиболее часто для обнаружения промаха используют так называемый критерий Райта. Согласно этому критерию, если случайное отклонение какого-либо измерения от среднего арифметического значения превышает Зs, то есть основание считать, что данное измерение содержит промах. Критерий Райта в таком виде целесообразно применять при не очень большом числе измерений (s? n? 20). Если же число измерений 20 < n? 100, то рекомендуется вместо значения Зs использовать значение 4s.
Более обоснованная, хотя и более громоздкая процедура исключения грубых погрешностей базируется на одном из разделов математической статистики—статистической проверке гипотез. В связи с тем что не предполагается знания читателем соответствующего материала, авторы вынуждены отослать интересующихся к одному из курсов, посвященных специально вопросу обработки экспериментальных результатов [28 ].
Необходимое число измерений. Вопрос о том, сколько измерений требуется произвести для того, чтобы погрешность не превышала допустимое значение, весьма важен, так как от его решения зависит весь последующий ход эксперимента.
Надо четко понимать, что увеличением числа измерений можно уменьшить только случайную составляющую погрешности (уменьшить средние квадратические погрешности s и s ср, которые согласно формулам (1.10) и (1.11) зависят от числа измерений n). В то же время систематическая погрешность не уменьшается при увеличении n. Поэтому если остаточная систематическая погрешность является преобладающей, то увеличение числа измерений мало что дает. Чаще всего в этом случае ограничиваются одним измерением. Так, например, при измерении напряжения сети неточным переносным стрелочным прибором нет никакого смысла прибегать к многократным измерениям и статистической обработке результатов измерения. Поскольку систематические погрешности заведомо превышают случайные, то достаточно провести всего одно измерение. При более точных измерениях на первый план могут выступить случайные погрешности. Тогда проведение многократных измерений является оправданным. Число измерений нужно выбрать таким, чтобы средняя квадратическая случайная погрешность s ср не превышала максимального допускаемого значения s ср, доп. Ясно, однако, что уменьшение s ср за счет многократных измерений следует добиваться только до тех пор, пока вклад случайных погрешностей в общую погрешность измерения не будет сравним со вкладом остаточных систематических погрешностей.
