Алгоритмы циклической структуры являются наиболее распространённым видом алгоритмов. В алгоритмахциклической структуры в зависимости от выполнения или невыполнения какого-либо условия выполняется повторяющаяся последовательность действий, называющаяся телом цикла.
Классическим примером использования структуры «Цикл» является задача табулирования функции. Задача табулирования (получение таблицы) некоторой функции y = f (x) сводится к вычислению значений этой функции при параметре цикла х, изменяющемся с постоянным шагом Dx в заданном диапазоне от начального значения аргумента xn до конечного значения xk. На экран монитора выводится ](xk – xn)/ Dx [+ 1 пар значений аргумента x с помощью оператора вывода, расположенного внутри тела цикла. Скобки ][ означают, что берётся целая часть от деления.
Пример. Вычислить значение функции y (x) = x 2+ 1,5 при изменении аргумента x в диапазоне xn ≤ x ≤ xk с шагом Dx. Вывести таблицу значений x и y.
Визуальное представление алгоритма решения задачи в виде цикла типа «ПОКА» с предусловием дано на рисунке 9.13
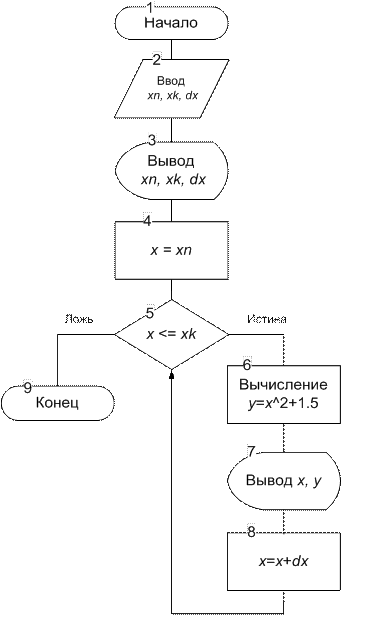
Рис. 9.13. Визуальное представление алгоритма табулирования функции в виде цикла типа «ПОКА» − цикл с предусловием
Это цикл с заданным числом повторений ](xk – xn)/ Dx [ + 1. Перед первым выполнением цикла необходимо задать начальное значение аргумента x, равное xn, а затем ](xk – xn)/ Dx [ + 1 раз выполнить вычисление и вывод значений функции y. При каждом новом выполнении цикла необходимо изменять аргумент на величину шага, равного Dx. Чтобы процесс не был бесконечным, необходимо задать условие повторения или окончания цикла.
В схеме циклического алгоритма присутствуют обязательные блоки в этих структурах: установка начального значения параметра (блок 4), проверка условия достижения конечного значения параметра (блок 5), изменение параметра (блок 8).
Телом данного циклического процесса являются блоки 5, 6, 7 и 8. Параметром данного цикла является переменная x.
Представим данную схему циклического алгоритма с помощью цикла типа «ДЛЯ», или цикла с параметром, который является модификацией цикла «ПОКА» для ситуации, когда заранее известно количество повторений некоторых действий. В этом случае все три необходимых блока – блок 4, блок 5 и блок 8 – собираются в один блок – блок 4 (рис. 9.14), в котором указываются начальное и конечное значения параметра и шаг изменения.
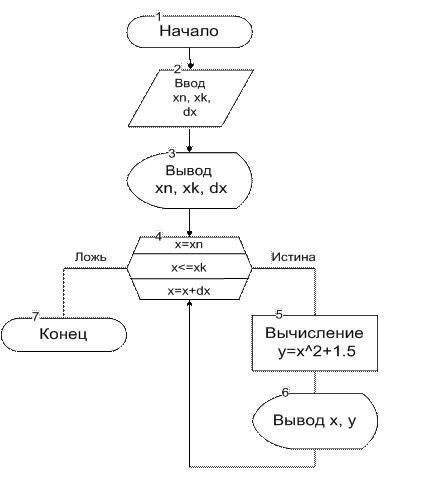
Рис. 9.14. Визуальное представление алгоритма табулирования функции в виде цикла типа«ДЛЯ», или цикла с параметром
На рисунке 9.14 блок 4 для большей наглядности изображён в «развёрнутом» виде. Общепринятым является компактное изображение такого блока в виде символа «Подготовка» (рис. 9.15). Именно такое представление мы будем использовать в дальнейшем. Если dx отсутствует, то по умолчанию dx = 1.

Рис. 9.15. Представление цикла с параметром символом «Подготовка»
Приведем несколько тестовых заданий с решениями.
Тестовое задание 9.9.
Укажите, какие результаты будут выведены на экран монитора при выполнении следующего фрагмента алгоритма (рис. 9.16):

Рис. 9.16. Рисунок к заданию 9.9
Решение
| Блок 1. Переменной x присваивается значение 5, x =5. | |
| цикл | Блок 2. Вычисляется значение переменной y = x 2+2=52+2=27. Блок 3. На экран монитора выводятся значения переменных x = 5 и y = 27. Блок 4. Переменной x присваивается новое значение: x = x + 2 = 5 + 2 = 7. Блок 5. Выполняется проверка условия x ≤ 10; подставляя новое значение x = 7, получим 7 ≤ 10; условие выполняется, следовательно, после блока 5 выполняется блок 2. |
| цикл | Блок 2. Вычисляется значение переменной с новым значением x = 7, y = x 2 + 2 = 72 + 2 = 51. Блок 3. На экран выводятся значения переменных x = 7 и y = 51. Блок 4. Переменной x присваивается новое значение: x = x + 2 = 7 + 2 = 9. Блок 5. Выполняется проверка условия x ≤ 10; подставляя новое значение x = 9, получим 9 ≤ 10; условие выполняется, следовательно, после блока 5 выполняется блок 2. |
| цикл | Блок 2. Вычисляется значение переменной с новым значением x = 9, y = x 2+2=92+2=83. Блок 3. На экран выводятся значения переменных x = 9 и y = 83. Блок 4. Переменной x присваивается новое значение: x = x + 2 = 9 + 2 = 11. Блок 5. Выполняется проверка условия x ≤ 10; подставляя новое значение x = 11, получим 11 ≤ 10; условие не выполняется, следовательно, после блока 5 выполняется выход из данного фрагмента алгоритма. |
Таким образом, данный фрагмент алгоритма описывает задачу табулирования (получение таблицы) функции y = f (х) = x 2+2. Вычисляются значения этой функции при параметре цикла х, изменяющемся с постоянным шагом Dx = 2 в заданном диапазоне от начального значения аргумента x n =5 до конечного значения xk = 10. На экран выводится ](xk – xn)/ Dx [+ 1=3 пар значений аргумента x с помощью блока вывода, расположенного внутри тела цикла. Результатом выполнения данного циклического алгоритма является следующий список значений (аргумента x и функции y):
5 27
7 51
9 83
Так как в алгоритме сначала выполняется действие, а потом проверка окончания циклического процесса, следовательно, в данном алгоритме реализована разновидность базовой управляющей структуры «цикл с постусловием» типа «ДО».
Блоки 2÷5 являются телом цикла. Переменная x − параметр цикла. Количество повторений цикла − 3.
Этот же алгоритм может быть реализован в виде «цикла с предусловием» (рис. 9.13) и «цикла с параметром» (рис. 9.14).
Тестовое задание 9.10.
Укажите, какие результаты будут выведены на экран монитора при выполнении следующего фрагмента алгоритма (рис. 9.17):
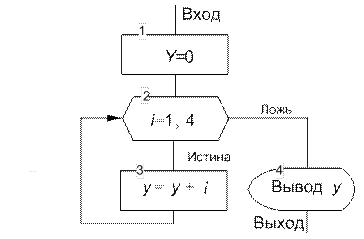
Рис. 9.17. Визуальное представление алгоритма накопления суммы
Решение.
| Блок 1. Переменной Y присваивается значение 0, Y = 0. | |
| цикл | Блок 2 представляет собой символ «подготовка». Его назначение − заголовок цикла (рис. 9.14, блок 4 и рис.9.15), в котором указывается начальное (i н=1), конечное значение параметра цикла i (iк =4) и шаг его изменения (i ш=1). Следовательно, на данном шаге параметр цикла принимает начальное значение i =1. Блок 3. Переменная y принимает новое значение y = y + i =0+1=1. После блока 3 выполняется блок 2. |
| цикл | Блок 2. Согласно назначению блока 2, который представляет собой заголовок цикла (рис. 9.15), на следующем этапе переменная цикла i принимает новое значение, увеличенное на шаг i = i +1=1+1=2, после этого проверяется условие окончания циклического процесса путем сравнения текущего значения параметра цикла i и его конечного значения − i ≤ 4? На данном этапе условие 2 ≤ 4 выполняется, следовательно, блок 3 повторяется для нового значения i. Блок 3. Переменная y принимает новое значение y = y + i = 1+2=3. После блока 3 выполняется блок 2. |
| цикл | Блок 2. Переменная цикла i принимает новое значение, увеличенное на шаг i = i +1=2+1=3, после этого проверяется условие окончания циклического процесса путем сравнения текущего значения параметра цикла i и его конечного значения − i ≤ 4? На данном этапе условие 3 ≤ 4 выполняется, следовательно, блок 3 повторяется для нового значения i. Блок 3. Переменная y принимает новое значение y = y + i =3+3=6. После блока 3 снова выполняется блок 2. |
| цикл | Блок 2. Переменная цикла i принимает новое значение, увеличенное на шаг i = i + 1 = 3 + 1 = 4, после этого проверяется условие окончания циклического процесса путём сравнения текущего значения параметра цикла i и его конечного значения − i ≤ 4? На данном этапе условие 4 ≤ 4 выполняется, следовательно, блок 3 повторяется для нового значения i. Блок 3. Переменная y принимает новое значение y = y + i =6+4=10. После блока 3 снова выполняется блок 2. |
| Блок 2. Переменная цикла i принимает новое значение, увеличенное на шаг i = i+1=4+1=5, после этого снова проверяется условие окончания циклического процесса путём сравнения текущего значения параметра цикла i и его конечного значения − i ≤ 4? На данном этапе условие 5 ≤ 4 не выполняется, следовательно, происходит окончание циклического процесса. После блока 2 в этом случае выполняется блок 4. | |
| Блок 4. На экран монитора выводится y = 10. |
Количество повторений цикла − 4.
Нетрудно увидеть, что в данном фрагменте описан алгоритм накопления суммы, в данном алгоритме y = 0+1+2+3+4.
Присвоение начального значения переменной y, в которой накапливается сумма, выполняется перед циклом. Вывод результата, поскольку он единственный, осуществляют после окончания работы цикла.
Тестовое задание 9.11.
Укажите, какие значения примут переменные a и b после выполнениия следующего фрагмента алгоритма (рис 9.18):

Рис. 9.18. Фрагмент схемы алгоритма к заданию 9.11
Решение.
Выполним алгоритм последовательно.
| Блок 1. а =1, b =1. | |
| цикл | Блок 2. a = 4? 1 = 4? Нет, следовательно, выполняем блок 3. Блок 3. a = a +1=1+1=2, b = b + a =1+2=3. После блока 3 согласно схеме алгоритма всегда выполняется блок 2. |
| цикл | Блок 2. a = 4?, 2=4? Нет, следовательно, выполняем блок 3. Блок 3. a = a +1=2+1=3, b = b + a =3+3=6. После блока 3 всегда выполняется блок 2. |
| цикл | Блок 2. a = 4? 3 = 4? Нет, следовательно, выполняем блок 3. Блок 3. a = a +1=3+1=4, b = b + a =6+4=10. |
| Блок 2 a=4? 4=4? Да, следовательно, происходит выход из цикла. |
Переменная b после окончания циклического процесса равна 10, а переменная а приняла значение 4. Данный алгоритм представляет собой «цикл с предусловием». Количество повторений тела цикла равно 3.






