Теоретическая часть. Изучение метода дифференциальных уравнений

РАСЧЕТ НАДЕЖНОСТИ ПРОЕКТИРУЕМЫХ СИСТЕМ

Цель работы

Изучение метода дифференциальных уравнений.

Теоретическая часть

Метод основан на допущении о показательных распределениях времени (наработки) между отказами и времени восстановления. Параметр потока отказов w=l=1/ m_t, интенсивность восстановления m=1/ m_tв, где m_t - среднее время до отказа (между отказами); m_tв - среднее время восстановления.

Метод дифференциальных уравнений может быть использован при расчете надежности как восстанавливаемых, так и невосстанав­ливаемых систем. Для применения метода необходимо иметь матема­тическую модель в виде множества состояний системы, в которых она может находиться при отказах и восстановлениях элементов.

Чтобы определить показатели надежности, составляют и реша­ют систему дифференциальных уравнений для вероятностей состоя­нии (уравнений Колмогорова).

Обычно предполагают, что отказавшие объекты начинают не­медленно восстанавливаться и отсутствует число ограничений на число восстановлений.

Математическую модель обычно изображают в виде графа (схемы) состояний, ниже приведен пример графа состояний.

l_n l₁

 

. m_n m₁

. m₃ l₃ m₂ l₂

.

 

При невосстанавливаемой системе между состояниями имеется лишь по одной стрелке.

Для определения вероятностей p_j(t) нахождения системы в момент времени t в j -м состоянии можно составить по графу состояний систему обыкновенных дифференциальных уравнений.

Для приведенного графа состояний имеем:

 

 

;

;

.

.

.

Уравнение для состояния 0 опускается из-за громоздкости. Система дифференциальных уравнений дополняется нормировочным условием .

Все множество возможных состояний системы разбивается на два: подмножество состояний n ₁, в которых система находится в работоспособном состоянии и n ₂ – подмножество неработоспособных состояний.

Когда выписывают коэффициент готовности или коэффициент простоя (перерывы в работе системы допустимы), рассматривают установившийся режим эксплуатации при . При этом все производные и система дифференциальных уравне­ний переходит в систему алгебраических уравнений.

Рассмотрим в качестве примера вычисление коэффициента готов­ности К _ГС системы, состоящей из n элементов, коэффици­енты готовности которых К _Г1, К _Г2, … К _Гn. При отказе одного из элементов отказывает вся система.

Граф состояний системы изображен выше. На графе обозначены следующие возможные состояния:

0 - все элементы работоспособ­ны;

1- элемент неработоспособен, остальные работоспособны;

2 - второй элемент неработоспособен, остальные работоспособны;

3 - третий элемент неработоспособен, остальные работоспособны и т.д.

Вероятности одновременного появления двух неработоспособных элементов пренебрежимо малы. Символами , ,… обозначены интенсивности отказов; 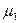, ,…, - интенсивности восстановления соответствующих элементов. При установившемся режиме эксплуатации

;

;

.

.

.

Решив полученную систему алгебраических уравнений, с учетом нормировочного условия получим

 

. (1)

Вероятность нахождения в j -м состоянии .

Из соотношения имеем: (2)

Подставив (2) в (1), получаем

.

Пусть, например, К _Г1=0,61; К _Г2=0,72; К _Г3=0,63.

Получаем

.