Параметры системы, определяющие ее состояние, с течением времени изменяют свои значения под воздействием множества факторов, которые носят случайный характер. С учетом воздействия дестабилизирующих факторов, процесс случайного дрейфа параметров может аппроксимировать в виде
,
где 
– 
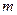-мерный случайный процесс дрейфа параметров;
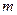– нестационарный (обычно монотонный) -мерный случайный процесс необратимых изменений значений параметров;
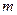– стационарный -мерный случайный процесс обратимого изменения значений параметров под воздействием внешних условий.
Необратимые изменения значений параметров в основном обусловлены деградационными процессами старения и износа, которые приводят к отказу системы. Обратимые изменения параметров являются стационарными процессами и могут рассматриваться как некоторая высокочастотная составляющая случайного процесса, обусловленная флуктациями внутренних факторов.
Процесс случайного дрейфа параметров может быть описан и в виде
, (3.1)
где 
– детерминированная составляющая 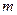-мерного случайный процесса необратимых изменений значений параметров;
– случайная составляющая 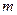-мерного случайный процесса, обусловленная воздействием внутренних и внешних факторов, а также погрешностями измерений.
Процесс дрейфа параметров (3.1) в зависимости от вида и величины составляющих и может быть описан различными способами. Например, (3.1) может быть представлено прогнозирующей функцией в виде ортогонального канонического выражения
, (3.2)
где 
– некоррелированные случайные величины, математическое ожидание которых равно 0;
– детерминированные функции времени, называемые ортогональными координатами.
При выборе вида прогнозирующей функции 
учитывается:
- характер протекающего процесса: эволюционный или возможен скачок;
- прошлый опыт, позволяющий определить, является ли прогнозирующая функция детерминированной, либо стохастической.
- степень изученности процесса, что эквивалентно виду математического описания;
- вид функции, описывающей детерминированную составляющую процессов старения и износа (тренд).
На рис 3.6 представлены возможные варианты прогнозирующей функции.
Рисунок 3.6 – Вид прогнозирующей функции
Следует обратить внимание на формулировки задач прогноза по применение различных алгоритмов, использующих знание прогнозирующей функции.
Например, при использовании алгоритмов экстраполяции задача формулируется следующим образом:
Дано: процесс, отображающий изменение состояния системы представлен в виде (3.1), который дискретно и непрерывно наблюдается на интервале времени 
и известны значения 
, 
,…, 
в моменты времени 
, 
,…, 
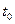, а также модель прогнозирования .
Найти: 
, при 
, т.е. 
, 
,…, 
в моменты времени 
, 
,…, 
.
При использовании алгоритмов статистической классификации задача формулируется иначе:
Дано: в начальный момент времени 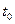или ограниченный начальный период времени известны значения , а также модель прогнозирования .
Найти: Принять решение о принадлежности системы к тому или иному классу 
. Классы могут устанавливаться по принадлежности значений параметров области работоспособности и (или) по принадлежности интервалу безотказной работы системы.
