Построение математических моделей для расчета показателей надежности по дереву отказов

 

Математические модели для расчета показателей надежности системы по ДО в соответствии с рекомендациями [25] могут быть получены с использованием булева представления ДО и применения метода минимальных сечений.

 

2.3.3.1 Булево представление дерева отказов. Пусть состояние системы задается некоторой функцией 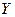. Предположим, что система с точки зрения надежности может находиться только в двух характерных состояниях: работоспособном () и неработоспособном ()

(2.7)

Допустим также, что состояние элементов и выполнение заданных условий описывается некоторым вектором

, (2.8)

где – переменная, характеризующая состояние -го элемента, либо выполнение -го условия (если -й номер условия), – общее число элементов системы и наложенных условий.

Пусть каждая переменная вектора принимает только два значения , либо . Равенство означает нахождение -го элемента в работоспособном состоянии, либо (если -й номер условия) – невыполнение наложенного условия. При -й элемент находится в состоянии отказа, либо выполнено -е условие.

Логической функцией работоспособности (ЛФР) системы будем называть функцию алгебры логики (ФАЛ), связывающую состояние элементов системы и выполнение некоторых заданных условий с работоспособным состоянием системы

. (2.9)

Функцию называют монотонной, если для любых наборов и , таких, что имеет место соотношение

. (2.10)

Объекты, удовлетворяющие этим условиям, называют системами с монотонной структурой. Иначе условие монотонности может быть представлено в следующей форме.

Объект будет обладать монотонной структурой при соблюдении следующих условий:

Если все элементы системы находятся в работоспособном состоянии, а все условия не выполнены, т.е. , то система находится в работоспособном состоянии.

Если все элементы отказали и все условия выполнены, то система переходит в состояние отказа.

Отказ, либо выполнение какого-либо условия, не может перевести систему в работоспособное состояние из неработоспособного, и, наоборот, восстановление отказа элемента для системы, находящейся в работоспособном состоянии, не может вызвать перехода ее в состояние отказа.

Все реальные технические системы с точки зрения перечисленных правил относятся, как правило, к системам с монотонной структурой.

Для монотонной структуры ЛФР системы можно записать с помощью минимальных путей (МП) или минимальных сечений (МС), которые несложно выделить при анализе конкретного дерева отказов.

Путем называется множество элементов , единичное состояние которых обеспечивает единичное состояние ЛФР. Иначе, путь – это набор элементов системы, находящихся в работоспособном состоянии и невыполненных условий, обеспечивающих работоспособное состояние системы.

Минимальным путем называется такая конъюнкция элементов и условий, когда ни одну из компонент нельзя изъять, не нарушив непредельного состояния системы.

Такая конъюнкция может быть записана в виде следующей ФАЛ

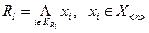, (2.11)

где – означает множество номеров, соответствующих пути .

Иначе, минимальный путь – это минимальный набор элементов и условий, работоспособное состояние (невыполнение условий) которых обеспечивает работоспособное состояние системы.

Сечением называется множество элементов , нулевое состояние которых обеспечивает нулевое состояние ЛФР.

Иначе, сечение – это набор элементов системы, отказ которых, и условий, выполнение которых, обеспечивают неработоспособное состояние системы.

Минимальным сечением системы называется такая конъюнкция отрицаний его элементов и условий, когда ни одну из компонент нельзя изъять, не нарушив состояния отказа системы.

Такая конъюнкция записывается в виде следующей ФАЛ

, (2.12)

где 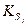– означает множество номеров, соответствующих сечению .

Добавление хотя бы одного элемента к МП или МС лишает их свойств минимальности, а удаление – свойств пути, или, соответственно, сечения.

Известно, что любой система с конечным числом элементов и наложенных условий имеет конечное число минимальных путей () и минимальных сечений ().

Тогда условие отказа системы может быть записано двумя различными способами:

а) через минимальные пути

(2.13)

в виде конъюнкции отрицаний всех имеющихся минимальных путей;

б) через минимальные сечения

(2.14)

в виде дизъюнкции всех имеющихся минимальных сечений.

В свою очередь, условия работоспособности имеют вид:

а) через минимальные пути

(2.15)

в виде дизъюнкции всех имеющихся минимальных путей;

б) через минимальные сечения

(2.16)

в виде конъюнкции отрицаний всех имеющихся минимальных сечений.

Отказ системы не достигается если

(2.17)

Соответственно, условия отказа системы:

(2.18)

Условие (2.12) означает, что в структуре ДО есть хотя бы один МП, либо нет ни одного МС. Условие (2.13) означает, что в структуре ДО нет ни одного МП, либо есть хотя бы одно МС.

Пример. Сформировать условия отказа и работоспособности для системы, ДО которой приведено на рис. 2.11.

Множество минимальных путей, определяемое при анализе ДО, имеет вид (для простоты здесь и далее операция конъюнкции будем обозначать знаком «умножения», т.е. ):

Множество минимальных сечений ДО имеет вид:

.

ЛФР системы может быть записана в соответствии с (2.15) как

,

либо в соответствии с (2.16) как

.

В соответствии с (2.13) имеем:

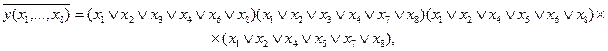
а в соответствии с (2.14)

.

Тогда в соответствии с (2.17) условия работоспособности можно представить как:

либо

либо

либо

.

В соответствии с выражением (2.18), следующие условия формируют условия отказа системы:

либо

либо

либо .

Для дальнейшего анализа может быть выбрана та форма задания условий отказа, которая является наиболее компактной, хотя все остальные формы полностью эквивалентны относительно конечного результата.

Таким образом, булево описание условия отказа системы позволяет наиболее полно, четко и однозначно представить причинно-следственные связи между неработоспособным состоянием системы и состояниями его элементов и другими факторами, определяющими надежность системы.

 

2.3.3.2 Построение вероятностной функции работоспособности системы. Выше показано, как представить в форме функций алгебры логики условия работоспособности системы. Рассмотрим особенности расчета вероятности безотказной работы системы по известным ФАЛ.

Введем следующие обозначения: – ВБР системы на интервале 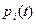– вероятность отсутствия начального события в ДО (ВБР -го элемента, либо вероятность невыполнения заданного условия).

Пусть известна ЛФР системы, описанная некоторой произвольной ФАЛ вида (2.9). Вероятностной функцией работоспособности (ВФР) системы будем называть вероятность истинности ЛФР

. (2.19)

Если ввести в рассмотрение вероятность наступления i-го события в ЛФР

тогда в предположении о независимости событий , функцию (2.19) можно преобразовать к виду

. (2.20)

Тогда можно сформулировать правило расчета ВБР: вероятность безотказной работы системы на интервале равна значению ВФР на этом интервале.

Таким образом, задача оценивания ВБР системы при известной ЛФР сводится к нахождению аналитического выражения для ВФР и подстановке в нее значений вероятностей (вероятностей событий, инверсных базовым событиям ДО), определенных на интервале .

Рассмотрим возможности определения вида выражения ВФР по ЛФР. В общем случае ЛФР представляет собой произвольную ФАЛ.

Из полученных ранее в теории надежности результатов известно, что существуют такие формы задания ФАЛ, которые допускают непосредственный переход в вероятностную функцию (ВФ) заменой логических переменных вероятностями , а логических операций – соответствующими арифметическими операциями. Такие ФАЛ называют формами перехода к замещению (ФПЗ).

Если ФАЛ представлена в ФПЗ, то переход к ВФ осуществляется по следующим правилам:

- каждая буква в ФПЗ заменяется вероятностью ее равенства единице, причем

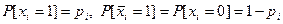; (2.21)

- отрицание функции заменяется разностью между единицей и вероятностью равенства этой функции единице, например

- операции логического умножения и сложения заменяются операциями арифметического умножения и сложения.

Существуют различные формы перехода к полному замещению. Прежде чем дать их характеристику, приведем ряд определений из алгебры логики [9], поясняющих используемые в дальнейшем понятия.

Выражение вида

(2.22)

называется элементарной конъюнкцией () ранга 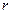, где – двоичная переменная величина, такая, что

В силу того, что , все символы в различны.

Выражение вида

, (2.23)

где – элементарные конъюнкции различных рангов, называется дизъюнктивной нормальной формой (ДНФ).

Если функция записана в ДНФ, причем ранг каждой элементарной конъюнкции равен , то такая ДНФ называется совершенной ДНФ (СДНФ).

Две элементарные конъюнкции называются ортогональными, если их произведение равно нулю.

ДНФ называется ортогональной ДНФ (ОДНФ) если все ее члены попарно ортогональны.

Бесповторной ДНФ называется такая ДНФ, в которой все буквы имеют разные номера.

Известно, что ФАЛ, записанные в СДНФ, ОДНФ или в форме бесповторной ФАЛ в базисе конъюнкция-отрицание, являются ФПЗ.

Приведем общий алгоритм преобразования ФАЛ произвольной формы к ФПЗ (рис. 2.14).

На первом этапе анализируется форма ФАЛ.

Рисунок 2.14 – Схема алгоритма преобразования ФАЛ к ФПЗ

 

Если ФАЛ является бесповторной, т.е. с неповторяющимися номерами переменных, то они преобразуются в ФПЗ по правилу де Моргана (к базису конъюнкция-отрицание).

При повторной форме ФАЛ она преобразуется в ДНФ и анализируется её вид. Если преобразованная ФАЛ имеет вид СДНФ, то ФПЗ получена, и можно формировать ВФР по правилам замещения. В противном случае используется ряд методов, к основным из которых относятся метод ортогонализации и метод разрезания.

Метод ортогонализации основывается на использовании следующих утверждений.

Отрицание элементарной конъюнкции ранга эквивалентно дизъюнкции

. (2.24)

В матричной форме записи логических функций данное преобразование имеет вид

.

(2.25)

Булева функция представляется в ДНФ в виде

(2.26)

и эквивалентна функции

, (2.27)

или в матричной форме записи:

.

(2.28)

Если вместо каждого выражения подставить его представление согласно (2.24), то после приведения дизъюнкции (2.27) к ДНФ (раскрытием скобок) получим ОДНФ булевой функции

(2.29)

где 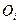– ортогональные члены функции , записанной в ОДНФ;

– число членов ОДНФ.

Преобразовав ЛФР к ОДНФ, можно приступить к формированию ВФР по правилам замещения.

Метод разрезания основывается на следующем утверждении.

Для любой структурной функции порядка справедливо следующее

Таким образом, если аргумент функции является совместной двоичной переменной, то преобразование (2.20) дает возможность перейти к дизъюнкции двух несовместных высказываний, причем в первое высказывание аргумент входит своим утверждением, а во второе – отрицанием. Функции отличаются от функции тем, что в них везде вместо аргумента подставлены соответственно 1 и 0.

Аргументы и можно принять за несовместимые гипотезы, образующие полную группу событий и, следовательно, есть все основания применять формулу полной вероятности. Необходимо также, чтобы функции были представлены в ФПЗ. С этой целью процедуру разрезания повторяют требуемое число раз.

На первом шаге разрезание функции производится по той из переменных, которая большее число раз встречается в выражении функции. После первого шага получают разложение (2.30). Затем функции упрощаются по правилам алгебры логики и анализируются на предмет наличия в них повторяющихся переменных. При их наличии, процедура разрезания применяется к

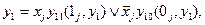
Операция разрезания проводится до тех пор, пока на очередном шаге не окажется, что ни в одну функцию ни одна переменная не входит более одного раза. Таким образом, получаем дизъюнкцию, каждый член которой представляет собой бесповторную ФАЛ, в общем случае произвольную.

Применив к , где – множество индексов типа 0, 1, 01, 11,… правило де Моргана, получим бесповторную ФАЛ в базисе конъюнкция-отрицание. Такая форма ФАЛ является ФПЗ.

Результатом выполнения разрезания исходная ФАЛ преобразуется к виду

где – число членов дизъюнкции;

– бесповторные ФАЛ в базисе конъюнкция-отрицание;

– несовместные гипотезы, образующие полную группу.

ВФР вычисляется по формуле полной вероятности

(2.30)

ФАЛ, характеризующие гипотезы и , представлены в форме бесповторной ФАЛ в базисе конъюнкция-отрицание, что позволяет далее применить правило замещения.

Пример. Рассмотрим ЛФР системы, составленную по ДО, приведенному на рис. 2.11. ЛФР, образованная на основе МС по правилу (2.16), имеет вид

.

В данной ФАЛ отсутствуют повторяющиеся элементы, поэтому она может быть преобразована к ФПЗ по правилу де Моргана

.

Далее по правилу замещения получаем выражение для ВФР

.

После преобразований окончательно получаем

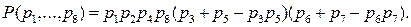(2.31)

ВБР с учетом (2.31) рассчитывается по формуле

(2.32)

 

Пример. Если в основу образования ЛФР положить правило (2.10), то ее выражение, как было показано выше, имеет следующий вид

. (2.33)

ФАЛ (2.33) является повторной и выражена в ДНФ (несовершенной). Поэтому применим алгоритм разрезания.

В выражении (36) переменные задействованы по четыре раза, а остальные по два. Разрежем ФАЛ (2.33) по переменной

.

Применив аналогичные преобразования относительно имеем

ФАЛ в круглых скобках является повторной и должна быть разрезана. Допустим разрезание произойдет относительно переменной

далее по

(2.34)

Преобразовав (2.34) получим

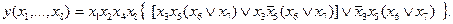(2.35)

Из (2.35) следует, что необходимо рассмотреть следующие гипотезы

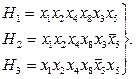(2.36)

Применив правило Де Моргана к выражению , получим

. (2.37)

С учетом (2.36), (2.37) ВФР имеет вид (см. (2.30))

Выполнив преобразования и раскрыв скобки, окончательно имеем:

(2.38)

(2.39)

 

Из сравнения (2.32) и (2.39) видно, что различная форма задания ЛФР системы приводит лишь к различиям в методах ее преобразования к ФПЗ, и не влияет на конечный результат определения вида ВФР.