При косвенных измерениях значение искомой величины получают на основании известной зависимости, связывающей ее с другими величинами, подвергаемыми прямым измерениям.
Вначале рассмотрим тот простейший случай, когда искомая величина Qz определяется как сумма двух величин Qx и Qy: Qz = Qx+ Qy
Поскольку результаты прямых измерений величин Qx и Qy (после исключения систематических погрешностей) включают в себя некоторые случайные погрешности, то формулу косвенного измерения суммы можно переписать в виде
,(*****)
где 
и 
– средние арифметические (или средние взвешенные), полученные при обработке результатов прямых измерений величин Qx и Qy, λX и λY – случайные погрешности средних арифметических, 
и λZ – оценка истинного значения косвенно измеряемой величины и его случайная погрешность.
Из уравнения (*****) непосредственно вытекает справедливость двух следующих равенств:
,
т.е. оценкой истинного значения косвенно измеряемой величины должна служить сумма оценок истинных значений исходных величин, случайные погрешности которых складываются.
Математическое ожидание оценки равно, очевидно, истинному значению искомой величины:
,
а ее дисперсия:
Входящее в это выражение математическое ожидание произведения случайных погрешностей называется корреляционным моментом и определяет степень “тесноты” линейной зависимости между погрешностями.
О наличии корреляции удобно судить по графику, на котором в координатах X, Y изображены пары последовательно получаемых результатов измерения величин QX и QY.
На рис.14 изображены случаи совместного распределения результатов измерения при положительной (рис.14,а) и отрицательной (рис.14,б) корреляции. Результаты измерений на рис.14,в некоррелированы.
а) б) в)
Рис. 14
Чаще всего наличия корреляции следует ожидать в тех случаях, когда обе величины измеряются одновременно однотипными измерительными средствами, причем неуловимые изменения внешних воздействий (электрических, магнитных, температурных и других полей, условий питания) одновременно заметно влияют на формирование случайных погрешностей их измерения. В некоторых случаях причиной корреляции между результатами измерений может стать сам оператор, поскольку при некоторых исследованиях, связанных с ручным уравновешиванием приборов сравнения (сличением мер на точных весах, в фотометрии), искусство и опыт наблюдателя оказывают значительное влияние на результаты измерений. В тех же случаях, когда исходные величины измеряют с помощью различных средств измерения в разное время, можно с полным правом ожидать, что результаты, если и будут коррелированы, то очень мало, и коэффициентом корреляции можно пренебречь.
Распределение результата косвенных измерений будет нормальным, если нормальны распределения результатов прямых измерений. В этих условиях для построения доверительного интервала, накрывающего истинное значение измеряемой величины, следует применить нормированную функцию нормального распределения, если число измерений достаточно велико. Если же объемы рядов прямых измерений недостаточно велики, то можно воспользоваться распределением Стьюдента с некоторым “эффективным” числом степеней свободы, которое для рассматриваемого случая при независимости погрешностей измерения (rXY=0) подсчитывается по формуле
,
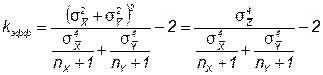где nX и nY – числа прямых наблюдений величин QX и QY.
Если числа наблюдений одинаковы (nX=nY=n), то выражение для эффективного числа степеней свободы распределения Стьюдента упрощается:
.
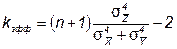Итоговый результат измерений записываем в виде:
,
где tp определяется из выражения:
.
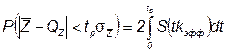Рассмотренные выражения можно использовать и в том случае, когда искомая величина является суммой от измеряемых прямыми способами величин:
.
К такой формуле приходим при измерении больших величин по частям, например при измерении длин с помощью концевых мер длины, взвешивании с применением набора гирь, измерении на электрических приборах сравнения с помощью магазинов сопротивлений, емкостей или индуктивностей, измерении объемов жидкостей мерниками меньшей вместимости и так далее. В этих случаях в качестве наиболее достоверной оценки 
истинного значения измеряемой величины 
принимается сумма оценок 
истинных значений слагаемых:
.
