В практике исследовательских работ часто встречаются ситуации, когда необходимо найти наиболее достоверное значение величины и оценить его возможные отклонения от истинного значения на основании измерений, проводимых разными наблюдателями с применением разнообразных измерительных средств и методов измерений в различных лабораториях или условиях внешней среды.
Ряды получающихся при этом результатов наблюдений называются неравнорассеянными, если оценки их дисперсий значительно отличаются друг от друга, а средние арифметические являются оценками одного и того же значения измеряемой величины.
Если средние неравнорассеянных рядов наблюдений мало отличаются друг от друга, то говорят о высокой воспроизводимости измерений, которая количественно характеризуется параметрами рассеивания результатов.
Рассмотрим некоторые случаи, приводящие к необходимости обработки результатов неравнорассеянных измерений:
1. Если при точных измерениях необходимо убедиться в отсутствии неисключенных систематических погрешностей, то измерения проводятся несколькими исследователями или группами исследователей. Если средние арифметические полученных рядов наблюдений незначительно отличаются друг от друга и ничто не указывает на наличие систематических погрешностей, то заманчиво объединить все полученные результаты и на основе их математической обработки получить более достоверные сведения об измеряемой величине.
2. Аналогичные измерения были выполнены в разных лабораториях различными методами и получены отличающиеся друг от друга результаты. Естественно и в этом случае, используя все имеющиеся данные, попытаться получить более достоверные значения измеряемых величин.
3. Измерения, относящиеся к образцовым мерам и измерительным приборам, часто повторяются через некоторое время. В конце концов, накапливаются ряды наблюдений и возникает необходимость объединить их. Точность рядов наблюдений различна, с одной стороны, из-за того, что для впервые проводимых измерений характерно большее рассеивание результатов, а с другой стороны, из-за того, что с течением времени средства измерения стареют или заменяются новыми.
Во всех описанных ситуациях приходится прибегать к методам обработки результатов неравнорассеянных рядов наблюдений, задача которых в общем случае заключается в нахождении наиболее достоверного значения измеряемой величины и оценки воспроизводимости измерений.
Основой для расчета служат следующие данные:
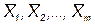
– средние арифметические m рядов равнорассеянных результатов наблюдений постоянной физической величины Q;
– среднеквадратические отклонения (или их оценки) результатов наблюдений в отдельных рядах;
– числа наблюдений в каждом ряду n1,n2,…nm; m – число рядов.
Если результаты наблюдений во всех рядах распределены нормально, то нормально распределены и все m средних арифметических 
с дисперсиями 
:
.
Q – истинное значение измеряемой величины (при условии, что систематические погрешности исключены).
Для практической обработки результатов неравнорассеянных рядов наблюдений необходимо ввести параметр вес отдельных средних арифметических:
.
Веса характеризуют степень нашего доверия к соответствующим рядам наблюдений. Чем больше число наблюдений в каждом данном ряду и чем меньше дисперсия результатов наблюдений, тем больше степень доверия к полученному при этом среднему арифметическому и с тем большим весом оно будет учтено при определении оценки истинного значения измеряемой величины
В соответствии со свойствами оценок максимального правдоподобия дисперсия среднего взвешенного должна равняться единице, деленной на математическое ожидание второй производной от логарифмической функции правдоподобия:
.
Отсюда следует, что дисперсия среднего взвешенного меньше дисперсии любого из исходных средних арифметических отдельных рядов наблюдений и поэтому при обработке неравнорассеянных рядов наблюдений точность измерений повышается.
Если теоретические дисперсии неизвестны, то пользуются их оценками, с помощью которых определяют веса или весовые коэффициенты.
При малом числе нормально распределенных результатов наблюдений пользуются распределением Стьюдента с числом степеней свободы
.
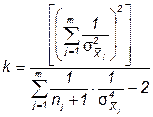Если же об исходных распределениях нет никаких заслуживающих внимания данных, то на основании центральной предельной теоремы можно все-таки предполагать, что распределение среднего взвешенного нормально, поскольку оно является суммой большого числа случайных величин с конечными дисперсиями и математическими ожиданиями
