По дисциплине

КОНСПЕКТ ЛЕКЦИЙ

«МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ»

Лекция 1 Предмет и задачи метрологии

Метрология – наука об измерениях, методах, средствах обеспечения их единства и способах достижения требуемой точности. Греческое слово «метрология» образовано от слов «метрон» - мера и «логос» - учение.

Метрология делится на три самостоятельных и взаимно дополняющих раздела, основным из которых является «Теоретическая метрология». В нем излагаются общие вопросы теории измерений. Раздел «Прикладная метрология» посвящен изучению вопросов практического применения в различных сферах деятельности результатов теоретических исследований. В разделе «Законодательная метрология» рассматриваются комплексы общих правил, требований и норм, а также другие вопросы, нуждающиеся в регламентации и контроле со стороны государства, направленные на обеспечение единства измерений и единообразие средств измерений.

Основное понятие метрологии – измерение. Согласно ГОСТ 16263-70, измерение – это нахождение значения физической величины (ФВ) опытным путем с помощью специальных технических средств.

Научный аспект измерений состоит в том, что с их помощью в науке осуществляется связь теории и практики.

Измерения обеспечивают получение количественной информации об объекте управления или контроля. Это составляет технический аспект измерений.

 

 

1.2 Структура теоретической метрологии.

Теоретическая метрология является основным разделом метрологии. Ее структура представлена в виде схемы.

 

1.1. Основные понятия и термины. Этот подраздел занимается обобщением и уточнением понятий, сложившихся в отдельных областях измерений с учетом специфики метрологии.

1.2. В постулатах метрологии развивается аксиоматическое построение теоретических основ метрологии.

1.3. Основной задачей учения о ФВ является построение единой системы ФВ, т.е. выбор основных величин системы и уравнений связи для определения производных величин.

1.4. В методологии измерений разрабатывается научная организация измерительных процессов. К числу основных направлений работ по методологии относятся:

1) переосмысление основ измерительной техники и метрологии в условиях обновления методов и средств измерений и широкого микропроцессорной техники;

2) структурный анализ измерительных процессов с системных позиций;

3) разработка новых подходов и организации процедуры измерений.

2.1. Основная цель подраздела Теории единиц ФВ – совершенствование единиц ФВ в рамках существующей системы величин.

2.2. В теории исходных средств измерений рассматриваются вопросы создания рациональной системы эталонов единиц ФВ, обеспечивающих требуемый уровень единства измерений.

2.3. Предметом изучения подраздела являются алгоритмы передачи размеров единиц ФВ.

3. В разделе обобщается опыт конкретных наук в области построения средств и методов измерений. В связи с развитием микропроцессорной и вычислительной техники и ее использование при построении СИ, важной задачей является разработка новых и совершенствование известных измерительных преобразователей.

4. В разделе обобщены методы, развиваемые в конкретных областях измерений. Включает 3 подраздела.

4.1. Является одним из центральных в метрологии, поскольку результаты измерений объективны настолько, насколько правильно оценены их погрешности.

4.2.1. Наиболее детально разработана в метрологии. Значительные знания накоплены и в конкретных областях измерений, на их основе развиты общение методы расчета погрешности СИ.

4.2.2. Также достаточно хорошо разработаны. Однако они требуют модификации с учетом специфики метрологии. К числу не до конца решенных задач следует отнести определение динамических характеристик СИ и градировочных характеристик первичных измерительных преобразователей.

4.2.3. Связана с общей теорией надежности. Однако специфика метрологических отказов делают невозможным автоматическое перенесение методов классической теории надежности в теорию метрологической надежности.

4.3.1. Посвящен разработке новых методов измерений и модификации существующих, что связано с ростом требований и точности измерений, диапазонам, быстродействию, условиям проведения измерений.

4.3.2. Основаны на методах, которые заимствуются из математики, физики и других дисциплин.

4.3.3. Область метрологии, которая активно развивается. К числу ее основных задач относятся уточнение метрологического содержания задач планирования измерений и обоснование заимствований математических методов из общей теории планирования эксперимента.

4.3.4. На данном уровне развития науки и техники позволяет решить такую главную задачу, как исследование предельной точности при помощи конкретных типов или экземпляров средств измерений.

 

Лекция 2. Основные понятия, связанные с объектами

измерений.

Все объекты окружающего мира характеризуются своими свойствами. Свойство – философская категория, выражающая такую сторону объекта, которая обуславливает его различие или общность с другими объектами и обнаруживается в его отношении к ним. Свойство – категория качественная. Для количественного описания различных свойств процессов и физических тел вводится понятие величины. Величина – это свойство чего-либо, которое может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, она имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной.

Анализ величин позволяет разделить их на два вида: реальные и идеальные.

 

 

Идеальные величины главным образом относятся к математике и являются обобщением (моделью) конкретных реальных понятий. Они вычисляются тем или иным способом.

Реальные величины делятся на физические и нефизические. ФВ может быть определена как величина, свойственная материальным объектам, изучаемым в естественных и технических науках. К нефизическим следует отнести величины присущие общественным наукам – философии, социологии, экономике и т.п.

Стандарт ГОСТ 16263 – 70 ФВ, как одно из свойств физического объекта, в качественном отношении общее для многих физических объектов, а в количественном - индивидуальное для каждого из них. Таким образом, ФВ – это измеренные свойства физических объектов или процессов, с помощью которых они могут быть изучены.

ФВ делятся на измеряемые и оцениваемые. Измеряемые ФВ могут быть выражены количественно в виде определенного числа установленных единиц измерений. Если для ФВ не может быть введена единица измерения, то тогда они могут быть только оценены. Оценивание величины осуществляется при помощи шкал. Шкала величин – упорядоченная последовательность ее значений, принятая по соглашению на основании результатов точных измерений. Нефизические величины могут быть только оценены, но это не входит в задачи теоретической метрологии.

 

Классификация ФВ

По видам явлений они делятся на следующие группы:

· вещественные, т.е. описывающие физические и физико–химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление, емкость, индуктивность и др.

· энергетические, т.е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относят ток, напряжение, мощность, энергия.

· характеризующие протекание процессов во времени. К этой группе относят спектральные характеристики, корреляционные функции и др.

По принадлежности к различным группам физических процессов ФВ делится на пространственно-временные, механические, тепловые, электрические и магнитные, акустические, световые, физико-химические, ионизирующих излучений, атомной и ядерной физики.

По степени условной независимости от других величин данной группы ФВ делится на основные, производственные и дополнительные. В настоящее время в системе СИ используется семь ФВ, выбранных в качестве основных: длина, время, масса, температура, сила электрического тока, сила света и количество вещества. Производные – это те, которые могут быть выраженные через основные. К дополнительным ФВ относятся плоский и телесный угла.

По наличию размерности ФВ делится на размерные и безразмерные (число пластичности). Физические объекты обладают неограниченным числом свойств, которые проявляются с бесконечным разнообразием. Среди множества специфических проявлений свойств есть и несколько общих. Н. Р. Кэмпбелл установил для всего разнообразия свойств Х объекта наличие трех наиболее общих проявление в отношениях эквивалентности, порядка и аддитивности. Отношение эквивалентности – это отношение в котором данное свойство Х у различных объектов А и В одинаково или неодинаково.

Примером объектов, обладающими свойствами эквивалентности, могут служить, например, виды животных: заяц, медведь и др. Каждая группа таких объектов отличается характерными свойствами, наименованиями. Для отображения числами данных объектов используется шкала наименований. Отношение порядка – отношение, в котором данной свойство Х у различных объектов оказывается больше или меньше.

Отношение аддитивности – отношение, когда однородные свойства различных объектов могут суммироваться. Кэмпбелл показал, что в зависимости от проявления наиболее общих отношений эквивалентности, порядка и аддитивности следует различать три вида свойств и величин Хэкв. – свойства, проявляющие себя только в отношении эквивалентности; Хинт – интенсивные величины, проявляющие себя в отношении эквивалентности и порядка, Хэкв – экстенсивные величины, проявляющие себя в отношении эквивалентности, порядка и аддитивности.

Примерами интенсивных величин служат твердость материала, запах и другие. Здесь вводится понятие ФВ и ее размер. Объекты, характеризующиеся интенсивными величинами, могут быть подвергнуты контролю. Контроль – процедура установления соответствия между состоянием объекта и нормой. Экстенсивные величины характеризуют физические, вещественные и энергетические свойства. Используется шкала интервалов. К ним относятся исчисление по различным календарям, температурные шкалы Цельсия, Фаренгейта и Реомюра.

 

Лекция 3. Основные понятия, связанные со средствами измерения.

Понятие «средство измерений» является одним из важнейших в метрологии. СИ – это техническое средство, используемое при измерениях и имеющие нормированные метрологические свойства.

Средство измерений является обобщенным понятием, объединяющим самые разнообразные конструктивно законченные устройства, которые реализуют одну из двух функций:

· воспроизводят величину заданного размера, например, гиря – заданную массу, магазин сопротивлений – ряд дискретных значений сопротивлений;

· вырабатывает сигнал (показание), несущий информацию о значении измеряемой величины. Показание СИ либо непосредственно воспринимаются органами чувств человека (показания стрелочного или цифрового приборов), либо они недоступны восприятию человекам и используются для преобразования другими СИ.

Последняя функция является основной и может быть реализована только посредством измерения. СИ должны содержать устройства, которые выполняют элементарные операции. В их число входят измерительные преобразователи, меры и устройства сравнения (компараторы).

Измерительный преобразователь – техническое устройство, построенное на определенном физическом принципе и выполняющее одно частное измерительное преобразование входного сигнала Х в выходной Хт.

Мера – средство измерений, предназначенное для хранения или воспроизведения ТВ одного или нескольких размеров.

Устройство сравнения - средство измерений, дающее возможность выполнять сравнение мер однородных величин или же показаний измерительных приборов.

 

X X₁=F(y) X_n-X₁/≤[Q]

 

X_M=N[Q]

Y=N₁

 

 

СИ могут работать в двух режимах: статическом и динамическом. Статический режим – такой режим, при котором изменением измеряемой величины за время, требуемое для проведения одного измерения, можно пренебречь.

В динамическом режиме такое пренебрежение недопустимо, поскольку указанное изменение превышает допустимую погрешность.

Основной характеристикой СИ в статическом режиме является функция (уравнение) преобразования. функция преобразования представляется в виде формулы, таблицы или графика.

Различают три вида функций преобразования: номинальную, индивидуальную, действительную. В статическом режиме выходной сигнал СИ в точности соответствует входному и следовательно коэффициент преобразования К равен номинальному коэффициенту К₀ во всем диапазоне изменения входной величины Х(t)

y (t) = K₀ X(t)

и соответствует идеальному безинерционному линейному преобразованию.

Реальные СИ обладают инерционным (динамическим) свойствам. Это приводит к более сложной зависимости между входными и выходными сигналами. Свойства СИ в динамических режимах описываются совокупностью динамических характеристик.

Основной у них является полная динамическая характеристика. В качестве нее используются: дифференциальные уравнения, переходную, импульсивную переходную, амплитудно-фазовую и амплитудно-частотные характеристики, совокупность амплитудно - частотной и фазочастотной характеристик, передаточную функцию.

Классификация СИ.

По роли выполняемой в системе обеспечения единства измерений, СИ делится на:

· метрологические, предназначенные для метрологических целей воспроизведения единицы и ее хранения или передачи размера единицы рабочим СИ;

· рабочие, применяемые для измерений, не связанных с передачей размера единиц.

Большинство принадлежит ко второй группе.

По уровню автоматизации делятся на три группы:

· неавтоматические;

· автоматизированные, производящие в автоматическом режиме одну или часть измерительной операции;

· автоматические, производящие в автоматическом режиме измерения и все операции, связанные с обработкой их результатов, регистрацией, передачей данных.

По уровню стандартизации СИ подразделяют на:

· стандартизированные, изготовленные в соответствии с требованиями государственного или отраслевого стандарта;

· не стандартизированные (уникальные), предназначенные для решения специальной измерительной задачи.

По отношению к измеряемой физической величине СИ делится на:

· основные – это СИ той физической величины, значение которой необходимо получить в соответствии с измерительной задачей.

· вспомогательные – это СИ той ФВ, влияние на основное СИ или объект измерения необходимо учесть для получения результатов измерения требуемой точности.

 

Классификация по роли в процессе измерения выполняемым функциями является основной. Ее можно представить в виде рисунка.

 

 

 

Лекция 4. Закономерности формирования результатов измерения,

понятие погрешности, источники погрешностей.

Измерение – сложный процесс, включающий в себя взаимодействие целого ряда его структурных элементов. К ним относятся измерительная задача, объект измерения, принцип, метод и средство измерения, и его модель, условия измерения, субъект измерения, результат и погрешность измерения.

Первым начальным элементом каждого измерения является его задача (цель). Задача любого измерения заключается в определении значения выбранной ФВ с требуемой точностью в задачных условиях. Постановку задачи осуществляет субъект измерения – человек. При постановке задачи конкретизируется объект измерения, в нем выделяется измеряемая ФВ и задается требуемая погрешность измерения. Взаимодействие субъекта с объектом возможно, но основе математический модели объекта.

Принцип измерений – совокупность физических принципов, на которых основаны измерения, например применение эффекта Джозефсона для измерения электрического напряжения.

Метод измерения – это прием или совокупность приемов сравнения измеряемой ФВ с ее единицей в соответствии с принципом измерения.

Метод измерений реализуется в средствах измерений.

В процессе измерения важную роль играют условия измерения – совокупность влияющих величин, описывающих состояние окружающей среды и средства измерений. Влияющая величина – это ФВ, не измеряемая данными СИ, но оказывающая влияние на его результаты.

Изменение условий измерения приводит к изменению состояния объекта измерения. Это оказывает влияние, но отклонение значения действительной величины от той, что была определена при формировании измерительной задачи. Влияние условий на СИ проявляется в изменении его метрологических характеристик. При этом часть погрешности, которая возникает из-за изменения условий, называется дополнительной погрешностью.

Различают нормальные, рабочие и предельные условия измерений.

Нормальные условия измерений задаются в нормативно – технической документации на СИ. υ = 220 ± 10%, ν = 50Гц ± 1%, t⁰ = 20⁰С, P = 760 мм. рт.ст.,Ψ = 60%, g = 9,8 м/с² .При нормальных условиях определяется основная погрешность данного СИ. При рабочих условиях нормируется дополнительная погрешность.

Предельные условия измерений – это условия, характеризуемые экстремальными значениями измеряемой и влияющих величин, которые СИ может выдержать без разрушений и ухудшения его метрологических характеристик.

Конечной целью любого измерения является его результат – значение ФВ, полученное путем ее измерения. Результат измерения представляется именованным или наименованным числом. Совместно с результатом измерений при необходимости приводят данные об условиях измерений.

При использовании термина «результат измерения» следует четко указать, к чему он относится: показанию СИ, исправленному или неисправленному результату, и проводилось ли усреднение результатов нескольких измерений. Исправленным результатом измерения называется полученное с помощью СИ значение величины и уточненное путем введения в него необходимых поправок на действие предполагаемых систематических погрешностей.

Качество измерений характеризуется точностью, достоверностью, правильностью, сходимостью и воспроизводимостью, а также размером допускаемых погрешностей. Точность измерения – характеристика качества измерения, отражающая близость к нулю погрешности его результата. Точность измерения является величиной качественной. Высокая точность соответствует малым погрешностям и наоборот. Иногда точность количественно оценивают обратной величиной модуля относительной погрешности. Например, если погрешность составляет 0,001, то точность равна 1000. Однако, количественная оценка точности широкого распространения не получила.

Достоверность измерений определяется степенью доверия к результату измерения и характеризуется вероятностью того, что истинное значение измеряемой величины находится в пределах. Данная вероятность называется доверительной.

Правильность измерений – это характеристика измерений, отражающая близость к нулю систематических погрешностей результатов измерений.

Сходимость результата измерения – характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, выполняемых одними и теми же методами в одних и тех же условиях. Сходимость измерений отражает влияние случайных погрешностей на результат измерения.

Воспроизводимость результатов измерения, полученных в разных местах, разными методами и СИ, но приведенных к одним и тем же условиям.

Количественная близость измеренного и истинного значения измеряемой величины описывается погрешностью результата измерений. Погрешность – это отклонение ∆Х результата измерения Хизм от истинного значения Хис измеряемой величины, определяемое по формуле ∆Х = Хизм – Хис.

Результат измерения и оценка его погрешности находится субъектом измерения с помощью вычислительных средств.

Субъект измерения объединяет в себе все ветви процесса измерения.

Классификация измерений

Наибольшее распространение получила классификация по общим приемам получения результатов измерений.

Измерения делятся на прямые, косвенные, совместные и совокупные.

Прямыми называются измерения, при которых искомое значение величины находят непосредственно по показаниям СИ. Например, масса, температура, напряжение.

Косвенные измерения – это измерения, при которых значение измеряемой величины находят на основании известной зависимости между ней и величинами, подвергаемыми прямым измерениям.

β = m/ν; R=υ/I

Совокупными называются проводимые одновременно измерения нескольких одноименных величин, при которых их искомые значения находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Совместными называются проводимые одновременно измерения двух или нескольких неодноименных величин для установления зависимости между ними.

По характеристике точности делятся на равноточные и неравноточные.

В зависимости от числа измерений различают однократные и многократные.

По отношению к изменению измеряемой величины делятся на технические и метрологические.

В зависимости от выражения результатов измерений делятся на абсолютные и относительные.

 

Лекция 5. Классификация погрешностей

Качество средств и результатов измерений характеризуется их погрешностями. Введение понятия погрешность требует четкого разграничения трех понятий: истинного и действительного значения измеряемой ФВ и результата измерений. Истинное значение ФВ – это значение, идеальным образом отражающее свойство данного объекта как в количественном, так и в качественном отношении. Оно является и абсолютной, и истинной. На практике это понятие заменяется понятием «действительное значение». Действительное значение – это значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него. Результат измерения представляет собой приближенную оценку истинного значения величины, найденную путем измерения.

Погрешность результата измерения – разница между результатом измерения Х и истинным значением Q измеряемой величины: ∆=X-Q.

Погрешность СИ – разность между показанием СИ и истинным значением измеряемой ФВ. Она характеризует точность результатов измерений, проводимых данным средством.

По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и грубые (промахи).

Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера ФВ, проведенных в одних и тех же условиях. В проявлении таких погрешностей не наблюдается какой-либо закономерности, они проявляются в виде разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения. Описание случайных погрешностей возможно только на основе математической статистики. Их нельзя исключить из результата измерений, но можно существенно уменьшить путем увеличения числа наблюдений.

Систематическая погрешность – составляющая погрешности, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ. Их отличительный признак заключается в том, что они могут быть предсказаны, обнаружены и поэтому почти полностью устранены путем введения соответствующей поправки.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени. Отличительные особенности:

· они могут быть скорректированы поправками только в данный момент времени, а далее вновь непредсказуемо изменяются.

Грубая погрешность (промах) – это случайная погрешность результата определенного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Они, как правило, возникают из-за ошибок или неправильного действия оператора. Возможной причиной возникновения промахов также могут быть кратковременные резкие изменения условий проведения измерений. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие отбрасывают.

По способу выражения различают абсолютную, относительную и приведенную погрешности.

Абсолютная погрешность описывается формулой ∆=X-Q и выражается в единицах измеряемой величины. Однако она не может в полной мере служить показателем точности измерений, т.к. одно и тоже ее значение, например ∆=0,05 мм при Х = 100 мм соответствует достаточно высокой точности измерений при Х = 1 мм – низкой. Поэтому вводится понятие относительной погрешности. Относительная погрешность – это отношение абсолютной погрешности измерения к истинному значению измеряемой величины.

Это характеристика точности результата не годится для нормирования погрешности СИ, т.к. при изменении значений Q принимает различные значения вплоть до бесконечности. В связи с этим используется еще одна разновидность погрешности – приведенная.

Приведенная погрешность – это относительная погрешность, в которой абсолютная погрешность СИ отнесена к условно принятому значению Q_N, постоянному во всем диапазоне измерений или его части

Условно принятое значение Q_N называют нормирующим. Чаще всего за него принимают верхний предел измерений данного СИ.

В зависимости от места возникновения различают инструментальные, методические и субъективные погрешности.

Инструментальная погрешность обусловлена погрешностью применяемого СИ. Иногда эту погрешность называют аппаратурой.

Отличительной особенностью методических погрешностей является то, что они не могут быть указаны в нормативно-технической документации на используемой СИ, а должны определятся оператором в каждом конкретном случае.

Субъективная (личная) погрешность обусловленная погрешностью отсчета оператором показаний по шкалам СИ, диаграммам регистрирующих приборов. Они вызываются состоянием оператора, его положением во время работы, несовершенством органов чувств.

По зависимости абсолютной погрешности от значений измеряемой величины различают:

· аддитивные ∆_а , не зависящие от измеряемой величины;

· мультипликативные ∆_м , которые прямо пропорциональны измеряемой величине;

· нелинейные ∆_н ,имеющие нелинейную зависимость от измеряемой величины.

По влиянию внешних условий различают основную и дополнительную погрешность СИ. Основной называется погрешность СИ, определяемая в нормальных условиях. Дополнительной называется погрешность СИ, возникающая вследствие отклонения какой-либо из влияющих величин.

В зависимости от влияния характера изменения измеряемых величин погрешности СИ делят на статические и динамические.

Правила округления результатов измерений

В окончательной записи погрешность измерения принято записывать с одной или двумя значащими цифрами. Установлены следующие правила округления значения погрешности и полученного результата:

1) Погрешность результата измерения указываются двумя значащими цифрами, если первая из них равна 1 или 2 и одной – если первая цифра равна 3 или более.

2) Результат измерения округляется до того же десятичного знакам, которым оканчивается округленное значение абсолютной погрешности.

3) Если цифра старшего из отбрасываемых разрядов < 5, то остальные числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.

4) Если цифра старшего из отбрасываемых разрядов ≥5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.

5) Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная и увеличивают на единицу, если она нечетная.

6) Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним – двумя лишними знаками.

 

 

Лекция 6. Обработка результатов измерений. Многократные

измерения.

Многократные измерения делятся на равно- и неравноточные. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. При равноточных измерениях СКО результатов всех рядом измерений равных между собой.

Задача обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится ее истинное значение.

Исходной информацией для обработки является ряд из n (n>4) результатов измерений х₁ , х₂ , х₃ , …. х_n, из которых исключены известные систематические погрешности, - выборка. Число n зависит как от требований и точности полученного результата, так и от реальной возможности выполнить повторные измерения.

Последовательность обработки результатов прямых многократных измерений состоит из ряда этапов.

Определение точечных оценок закона распределения результатов измерений. На этом этапе определяется:

· среднее арифметическое значение ;

· СКО результаты измерения S_x по формуле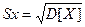

· СКО среднего арифметического значения

Грубые погрешности и промахи исключаются.

 

Определение закона распределения результатов измерений или случайных погрешностей измерений.

От выборки результатов измерений Х₁ , Х₂ , Х₃ , …. Х_n не переходят к выборке отклонений от среднеарифметического ∆ Х₁ ,∆ Х₂ ,∆ Х₃ , …∆ Х_n, где ∆Х_i = X_i-

Первым шагом является построение вариационного ряда от Х_min до Х_max.

Далее этот ряд разбивается на оптимальное число интервалов шириной

. Для числа измерений n = 40÷100, m = 7÷9

100÷500, m = 8÷12

500÷1000, m = 10÷16

Обычно не принимается от 6 до 12.

m_min = 0,55n^0,4 , m_max = 1,25n^0,4 . Искомое значение m должно быть нечетным. Полученное значение h всегда округляют в большую сторону.

Далее определяют интервалы группирования экспериментальных данных в виде ∆1=(Х, Х+h); ∆2=(Х₁+h; X+2h); …; ∆m=(y_n-h, y_n) и подсчитывают число попаданий n_k (частоты) результатов измерений в каждый интервал. Сумма n_k должна равняться n. По полученным значениям рассчитывают вероятности попадания результатов измерений (частости) в каждый из интервалов группирования по формуле:

Р_к = n_k/n, где k=1,2,…,m

После расчетов строят гистограмму, полигон и кумулятивную кривую.

По оси Х откладывают интервал ∆k, и на каждом интервале строится прямоугольник высотой Р_к. Площадь, заключенная под графиком, пропорциональна числу наблюдений.

Полигон представляет собой ломанную кривую, соединяющую середины верхних оснований каждого столбца гистограммы. Она более наглядно отражает форму кривой распределения. В результате совместно с осью Х образуется замкнутая кривая, площадь которой должна быть равна 1 (или числу наблюдений при использовании частостей).

Кумулятивная кривая – это график статистической функции распределения. Для ее построения по оси Х откладывают интервалы ∆k в порядке возрастания и на каждом интервале строят прямоугольник высотой

Значение F_k называется кумулятивной частостью, а сумма n_k кумулятивной частотой.

По виду построенных зависимостей может быть оценен закон распределения результатов измерений.

При n>50 оценка закона распределения ведется по критерию Пирсона или критерию Мизеса-Смирнова (ω₂).

c²=

 

При 50>n>15 применяется составной критерий (d-критерий), приведенный ГОСТ8.207 – 76.

При n<15 принадлежность экспериментального распределения к нормальному не проверяется.

Определение доверительных границ погрешности результата измерения ∆p

∆p = ±t_p · S , где

t_p - критерии распределения Стьюдента (прил.1) зависящий от доверительной вероятности и числа наблюдений.

Запись результата измерения

Результат измерений записывается в виде х = ± ∆p при доверительной вероятности Р=Р_д.

 

Функциональные и корреляционные зависимости

 

Зависимость называется функциональной, если каждому значению переменной величины Х соответствует одно или несколько определенных значений Y. В первом случае функция называется однозначной, во втором – многозначной.

Наряду с функциональными зависимостями в математической статистике рассматривают так называемые корреляционные зависимости, которые по своей природе относят к стохастическим (вероятностным) связям.

Вероятностная связь – это связь между случайными величинами. Она возникает под влиянием случайных факторов двух видов: разных для каждой случайной величины в отдельности и общих для всех сопряженных между собой случайных величин.

Например, если Х представляет собой некоторую функцию случайных величин V₁, V₂,…, V_k; Z₁, Z₂,…,Z_m, а Y – функцию тех же случайных величин V₁, V₂,…, V_k и некоторой другой совокупности U₁, U₂,…,U_n, то величины Х и Y будут стохастически взаимосвязаны. Наиболее простой является корреляционная связь.

 

 

 

Данные графики позволяют судить о наличии и форме корреляционной зависимости между случайными величинами X и Y. Прямые линии отражают предполагаемую зависимость между ними – линии регрессии. Они характеризуют форму связи между случайными величинами X и Y и строятся на основе выявления регрессионных связей, под которыми понимаются связи между фиксированными значениями одной случайной величины X_i и условными средними значениями другой Y_ini.

Задачей корреляционного анализа, наряду с установлением конкретной формы зависимости между случайными величинами X и Y с помощью линий регрессии, является также установление силы и тесноты связи этих величин.

Наиболее простой корреляцией является линейная корреляция. Она соблюдается точно в том случае, когда линии регрессии y = (x) и x = (y) являются линейными функциями. Коэффициент корреляции r характеризует меру линейной связи между случайными величинами X и Y. Он являются одним из самых распространенных способов измерения связи между ними.

При вычислении корреляционных характеристик поступают следующим образом:

1. Вычисляют ковариацию (момент связи) – простейшую характеристику связи между случайными величинами Х и Y.

 

 

2. Вычисляют коэффициент корреляции

 

 

3. Определяют коэффициенты для линий регрессии

 

 

4. Записывают уравнения регрессии, которые примут следующий вид

 

 

5. Определяют СКО для линий регрессии

 

 

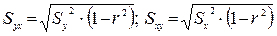
6. Определяют ширину доверительного интервала для линий регрессии

 

7. Строят линии регрессии.

 

Коэффициент корреляции r находится в пределах -1 < r < 1. При r=0 случайные величины X и Y и не коррелированны, а при |r| = 1между ними наблюдается линейная функциональная связь. Чем ближе r к единице, тем теснее линейная связь между величинами X и Y. Обычно считают, что при r=0,5– теснота связи удовлетворительная, а при r=0,8 … 0,85– хорошая.

Линейная корреляция является частным случаем корреляции. В случае корреляции более сложного вида связь между случайными величинами характеризуется корреляционным отношением. При одновременном исследовании трех и более случайных величин применяется множественная корреляция.

 

Правила отбраковки результатов измерений

Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат возникающий с вероятностью q≤0,003 маловероятен и его можно считать промахом, если | - X_i| ≥3S_x,где S_х – оценка СКО измерений. Величины - S_x вычисляют без учета экстремальных значений. Данный критерий надежен при числе измерений n≥20…50. При 6<n≤100 – 4S_x; 100<n≤1000 – 4,5S_x; при 1000<n≤10000 – 5S_x.

Критерий Романовского применяется, если число измерений n<20. При этом вычисляется отношение

β=

и сравнивается с критериями β_T, выбранным по таблице. Если β≥β_T, то результат X_i считается промахом и отбрасывается.

Критерий Шарлье, вариационный критерий Диксона, критерий Стьюдента.

Лекция 7. Государственная система обеспечения единства измерений (ГСИ). Метрологическое обеспечение

Под метрологическим обеспечением понимается установление и применение научных и организационных основ, технических средств, правил и норм, необходимых для достижения единства и требуемой точности измерений. Нормативной базой метрологического обеспечения являются стандарты ГСИ. К основным задачам стандартизации в области метрологического обеспечения относятся:

· совершенствование системы метрологического обеспечения, создание и совершенствование этапов единиц ФВ, а также методов и средств измерений высшей точности;

· установление норм, требований и методов в области проектирования и производства;

· установление единых систем документации, в том числе унифицированных;

· установление единых терминов и обозначений;

· установление единых правил выполнения всех работ по обеспечению единства измерений;

· своевременное изменение и дополнение правил законодательной метрологии в соответствии с новейшими открытиями и достижениями;

· постоянный контроль за выполнением правил законодательной метрологии;

· установление прав и обязанностей государственных и ведомственных органов метрологической службы по обеспечению единства измерений.

В нормативных документах ГСИ принято выделять базовые, на основе которых разрабатываются все остальные документы для конкретных областей измерений, измерительных процессов и средств измерений. Основополагающим базовым стандартом ГСИ является ГОСТ 8,417 – 82 ГСИ. «Единицы физических величин». Воспроизведение единиц осуществляется эталонами (3 ГОСТа).

Передача информации о размере единицы от эталонов средствам измерений регламентирована шестью базовыми стандартами. ГОСТ 8,061-80 ГСИ «Проверочные схемы. Содержание и построение». Устанавливает разделение поверочных схем на государственные - возглавляемые государственным эталоном и их охватывающие все СИ данной ФВ; ведомственные – возглавленные рабочим эталоном или образцовым средством высшего разряда и распределяющиеся на СИ, находящиеся в обращении внутри министерства (ведомства), и локальные – возглавляемые образцовым средством и предназначенные для СИ, подлежащих поверке в определенном органе Государственной или ведомственной метрологической службы.

Группы базовых стандартов устанавливают порядок нормирования метрологических характеристик СИ; правила выполнения и оформления результатов измерений; обеспечивают единообразие СИ; метрологический надзор за разработкой, состоянием и применение СИ; достоверные данные о физических константах и свойствах веществ и материалов.

К базовым стандартам относится также ГОСТ 16263-70. ГСИ «Метрология. Термины и определения».

Остальные государственные стандарты относятся к рабочим документам ГСИ, и делится на 4 группы:

1. Стандарты государственных эталонов и государственных поверочных схем.

2. Стандарты методов и средств поверки мер и измерительных приборов. В этой группе учитываются требованиями стандартов, регламентирующих технические требования к средствам измерений.

3. Стандарты норм точности измерений

4. Стандарты типовых методик выполнения измерений.

Положения ГОСТов конкретизируются с учетом выпускаемой продукции, особенностей технологических процессов и общей специфики производства в отраслевых и республиканских стандартах, методиках, методических указаниях, инструкциях и других рабочих документах ГСИ, входящих в систему нормативно-технической документации по метрологическому обеспечению.

 

Лекция 8. Структура и функции метрологической службы

Метрологическая служба – совокупность субъектов деятельности и видов работ, направленных на обеспечение единства измерений. В настоящее время метрологическая служба России состоит из Государственной метрологической службы, а также из метрологических служб органов государственного управления и юридических лиц.

Государственная метрологическая служба включает: государственные научные метрологические центры (ГНМЦ); органы Государственной метрологической службы на территориях республик в составе РФ, автономных областях, автономных округов, областей, городов Москвы и Санкт-Петербурга.

В состав Государственной метрологической службы входит 7ГНМЦ (Москва, Санкт-Петербург, Московская область, Новосибирск, Екатеринбург, Казань, Иркутск). ГНМЦ несут ответственность за создание, совершенствование, хранение и применение государственных эталонов, а также за разработку нормативных документов по обеспечению единства измерений. Научные центры являются хранителями государственных эталонов, проводят исследования в области теории измерений, разработки научно-методических основ совершенствования Российской системы измерений

Органам Государственной метрологической службы являются центры стандартизации, метрологии и сертификации – ЦСМиС, расположенные по всей территории России (их более 100) органы Государственной метрологической службы проводят работы по поверке и калибровке средств измерений, осуществляют контроль и надзор за обеспечением единства измерений.

Обеспечением единства измерений заняты и другие государственные службы: Государственная служба времени и частоты и определения параметров Земли (ГСВЧ) Государственная служба стандартных образцов состава и свойств веществ и материалов (ГССО), Государственная служба стандартных справочных данных о физических константах и свойствах веществ и материалов (ГСССД). Госстандарт России осуществляет координацию их деятельности.

Метрологические службы государственных органов управления и юридических лиц создаются для выполнения работ по обеспечению единства измерений, повышения уровня метрологического обеспечения. Допускается возложение отдельных функций метрологической службы на иные структурные подразделения. Метрологические службы государственных органов управления и юридических лиц организуют свою деятельность на основе положений закона РФ «Об обеспечении единства измерений», а других законодательных и нормативных документов, регламентирующих вопросы метрологии. Основные задачи, права и обязанности метрологических служб, государственных органов управления и юридических лиц любых форм собственности определены в Правилах по метрологии ПР 50,732 – 93 «ГСИ. Типовое положение органов в метрологической службе государственных органов управления и юридических лиц».

Метрологическая служба государственного органа управления представляет собой систему, образуемую приказом его руководителя, которая может включать: подразделение (службу главного метролога в центральном аппарате; головные и базовые организации метрологической службы в отраслях; метрологические службы предприятий).

К основным задачам метрологических служб относятся:

1. Калибровка СИ;

2. Надзор за состоянием и применением СИ за аттестованными методиками выполнения измерений, эталонами единиц величин, применяемыми для калибровки СИ, за соблюдение метрологических правил и норм, нормативных документов по обеспечению единства измерений;

3. Выдача обязательных предписаний, направленных на предотвращение, прекращение или устранения нарушений метрологических правил и норм.

4. Проверка своевременности, предоставленная СИ на испытания в целях утверждения типа СИ, а также на проверку и калибровку;

5. Анализ состояния измерений, испытаний и контроля на предприятии, в организации.

Метрологические службы предприятий должны уделять особое внимание состоянию измерений, соблюдение метрологических правил и норм в сферах деятельности предприятия, предусмотренных законом (ст. 13): при испытаниях и контроля качества продукции в целях определения соответствия обязательных требованиям госстандартов, при выполнении предприятием работ по обязательной сертификации продукции и услуг и др.

Специалисты метрологических служб предприятия должны принимать активное участие в аттестации испытательных подразделений, в подготовке к сертификации систем качества.

Метрологические службы могут быть аккредитованы на техническую компетентность в осуществлении конкретной деятельности в области обеспечения единства и требуемой точности измерений.

Основные понятия, связанные со стандартизацией.

Стандартизация – деятельность, направленная на разработку требований, норм, правил, обязательные для выполнения ему рекомендательных, обеспечивающих право потребителя на приобретение продукции надлежащего качества, за приемлемую цену, а также безопасность и комфортность труда. Стандартизация в России осуществляется в целях обеспечения:

· безопасности продукции, работ и услуг для окружающей среды, жизни, здоровья и имущества;

· технической и информационной совместимости, а также взаимозаменяемости продукции;

· качества продукции, работ и услуг в соответствии с уровнем развития науки, техники и технологии;

· единства измерений;

· экономии всех видов ресурсов;

· безопасности хозяйственных объектов с учетом строф и других ЧС.

· обороноспособности и мобилизационной готовности страны.

Объект стандартизации – конкретная продукция, конкретные услуги, конкретные работы или их группы.

Нормативный документ по стандартизации – это документ, содержащий правила, общие принципы, характеристики, касающиеся объектов стандартизации, определенных видов деятельности или их результатов, и доступных широкому кругу пользователей.

К нормативным документам по стандартизации в России относятся стандарты, технические регламенты, общероссийские классификаторы технико-экономической информации, а также правила по стандартизации.

Основной стандарт – Государственный стандарт РФ – стандарт, принятый Государственным комитетом РФ по стандартизации, метрологии и сертификации (Госстандарт России) или Государственным комитетом РФ по жилищной и строительной политике (Госстрой России). Разрабатывается на конкретные продукции, услуги, производственные процессы и их группы, имеющие преимущественно (рассказать про Госстандарт и Госстрой, ISO.)

 

СЕРТИФИКАЦИЯ

Слово «сертификат» в переводе с латинского означает «Сделано правильно». Когда этот термин применяется к продукции, то с его помощью может быть установлен изготовитель данного товара, название фирмы, ее юридический адрес и т.д. Этот вид сертификата называется сертификатом происхождения. Другой сертификат называется сертификат качества. В этом документе производитель указывает количественные характеристики различных свойств продукции, характеризующих ее качество. Сертификат качества имеет характер выборочной информации и используется изготовлением в настоящее время преимущественно в рекламных целях.

Наиболее широкое распространение получим сертификат соответствия, и именно его имеют ввиду, когда применяют термин «сертификат». Отличительная его особенность в том, что он является документальным результатом проведения специальной процедуры, называемой сертификацией соответствия.

. В мировой и отечественной практике применяются различные методы подтверждения соответствия объектов заданным требованиям, которые выполняются разными сторонами – изготовителями, продавцами, заказчиками, а также независимыми от них структурами.

Под сертификацией понимается действие третьей стороны, доказывающее, что должным образом идентифицированные продукция, процесс или услуга соответствуют конкретному стандарту или другому документу.

Законодательная база сертификации

В соответствии с Законом РФ «О сертификации продукции и услуг» целями сертификации являются: содействие потребителям в компетентном выборе продукции, защита их от недобросовестности изготовителя, контроль безопасности продукции для окружающей среды, жизни, здоровья и имущества, подтверждение показателей качества продукции, заявленных изготовителем. Закон «О защите прав потребителя», «О сертификации продукции и услуг», «О стандартизации», «Об обеспечении единства измерений».