Надійний інтервал. Перевірка статистичних гіпотез
Мета роботи:
навчитися застосовувати розрахунки надійного інтервалу випадкових величин з метою аналізу відповідності ознак друкованих та мультимедійних видань їхнім нормативам;
набути досвіду перевірки статистичних гіпотез стосовно рівня якості технологічних процесів у сфері поліграфії та мультимедіа.
Навчальний матеріал
1. Приклади законів розподілу деяких випадкових величин
Рівномірний розподіл. Рівномірний розподіл ймовірності є простим і може бути як дискретним, так і неперервним.
Дискретний рівномірний розподіл – це такий розподіл, для якого усі значення випадкової величини є рівноймовірними:
,
де k – кількість можливих значень випадкової величини.
Розподіл вірогідності неперервної випадкової величини Х, яка приймає значення з відрізку [а, b], називається рівномірним, якщо щільність розподілу випадкової величини на цьому відрізку є постійною, а поза ним дорівнює нулю (рис. 4-5):
| (8) |
Рис. 4. Графік функції F(x) рівномірного розподілу
Рис. 5. Графік функції f(x) рівномірного розподілу
Для рівномірного розподілу випадкової величини Х математичне сподівання є серединою відрізку [а; b]:
 ,
| (9) |
 .
| (10) |
Нормальний розподіл. Нормальним називається розподіл ймовірності неперервної випадкової величини, який описується щільністю ймовірності
 ,
| (11) |
де:
m – математичне сподівання випадкової величини,
– середньоквадратичне відхилення випадкової величини.
Нормальний закон розподілу займає центральне місце в теорії ймовірності і математичній статистиці. Це обумовлено тим, що нормальний закон проявляється у всіх випадках, коли випадкова величина є результатом дії великого числа різних чинників. Наприклад, помилки вимірювань розподілені за нормальним законом.
На практиці багато випадкових величин розподілені нормально або майже нормально: помилки стрільби; відхилення напруги в мережі від номіналу; сумарна виплата страхового товариства за довгостроковий період; дальність польоту снаряду; зріст чоловіків (жінок) одного віку і національності, й тому подібне (рис 6).
Рис. 6. Графік щільності розподілу випадкової величини, розподіленої за нормальним законом
Для випадкових величин, які розподілені за нормальним законом, діє правило трьох сигм.
Правило трьох сигм: якщо випадкова величина розподілена за нормальним законом, то ймовірність її відхилення від свого математичного сподівання на величину більше ніж 3 , (де – середньоквадратичне відхилення випадкової величини), близька до нуля (точніше, дорівнює 0,0027). Іншими словами, практично достовірно, що нормальна випадкова величина приймає значення з інтервалу [m-3 , m+3 ] (ймовірність цього дорівнює 0,9973).
2. Надійний інтервал випадкової величини
Надійний інтервал D випадкової величини з рівнем довіри (надійністю) g – це інтервал, який з ймовірністю g покриває всі вибіркові значення випадкової величини. Тобто всі вибіркові значення випадкової величини з ймовірністю g потрапляють в діапазон 
, де 
– вибіркове середнє (рис. 7).
Інтервал D для випадкової величини, яка має нормальний розподіл, визначається за формулою:
| D = s · z, | (12) |
де:
s – середнє квадратичне відхилення;
z – аргумент функції Лапласа, який визначається за допомогою відповідної таблиці для функції Лапласа Ф(z): вибирається таке z, для якого виконується умова: Ф(z) = g/2, де g – надійна ймовірність.
Таблицю зі значеннями функції Лапласа подано у Додатку А.
Якщо не відоме середнє квадратичне відхилення σ, то у формулі розрахунку використовується виправлене вибіркове середнє квадратичне відхилення s та коефіцієнт Стьюдента t:
| D = s · t, | (13) |
де:
t – коефіцієнт Стьюдента, який вибирається з відповідної таблиці залежно від значення надійної ймовірності g і кількості ступенів свободи (кількість ступенів свободи дорівнює n –1).
Таблицю зі значеннями коефіцієнту t розподілу Стьюдента подано у Додатку Б.
Зауважимо, що при розрахунках надійного інтервалу для малої вибірки (при n<30) також використовується коефіцієнт Стьюдента t (а не аргумент функції Лапласа).
Рис. 7. Приклади надійних інтервалів із різними значеннями надійної ймовірності
Надійний інтервал Dм математичного сподівання випадкової величини – це інтервал, який з великою ймовірністю містить значення математичного сподівання випадкової величини.
Надійна вірогідність gм – це ступінь упевненості в тому, що довірчий інтервал міститиме дійсне (невідоме) значення математичного сподівання генеральної сукупності.
Величина надійного інтервалу Dм залежить як від надійної ймовірності gм, так і від об'єму вибірки n:
Dм=  .
| (14) |
Приклад 1. Б уло здійснено вибірку 1600 осіб із сукупності усіх передплатників журналу «Видавничий бізнес». Середній вік за вибіркою – 30 років, середньоквадратичне відхилення – 10 років. Необхідно знайти надійний інтервал математичного сподівання.
Перш за все, необхідно задати надійну ймовірність оцінки. Візьмемо 95% надійність. Оскільки вибірка велика, скористаємося таблицею значень функції Лапласа (див. Додаток А) і знайдемо коефіцієнт довіри z=1,96. Тоді розрахуємо надійний інтервал D випадкової величини за формулою (11):
D= 1,96*10=19,6.
Залишилося розрахувати надійний інтервал математичного сподівання формулою (13):
Dм= 
=0,49.
З ймовірністю 95% істинний середній вік у генеральній сукупності знаходиться в інтервалі від 29,51 років до 30,49 років.
3. Перевірка статистичних гіпотез
Статистичною гіпотезою називають деяке твердження щодо значення (або значень) якого-небудь параметра випадкової величини. Наприклад, твердження M(Х)=5 (гіпотеза про те, що математичне сподівання дорівнює п'яти) або твердження D(Х)=D(Y) (гіпотеза про рівність двох дисперсій).
Під процедурою перевірки статистичних гіпотез розуміють послідовність дій, які дозволяють з тією або іншою мірою достовірності підтвердити або спростувати гіпотезу.
Формалізація статистичних гіпотез з математичної точки зору приводить до описання гіпотез двох видів:
Н0 – нульова гіпотеза,
Н1 – альтернативна гіпотеза.
Нульова гіпотеза (Н0) формулюється як гіпотеза про відсутність відмінностей у вибірках, про схожість двох розподілів і тому подібне. Альтернативна гіпотеза (Н1) протилежна за смислом і означає відмінність у вибірках, відмінність двох розподілів і тому подібне. Дві гіпотези утворюють повну групу несумісних подій: якщо приймається одна, то інша відхиляється.
Гіпотези перевіряються за допомогою статистичних критеріїв.
Статистичний критерій – це правило, яке дозволяє приймати істинну і відхиляти помилкову гіпотезу з високою ймовірністю. Математично критерій є формулою, результатом розрахунків за якою є деяке число. Критерій є випадковою величиною, розподіл якої залежить від числа ступенів свободи.
Для встановлення схожості-відмінності середніх арифметичних значень в двох вибірках (які вибираються з генеральних сукупностей, що мають нормальний розподіл) використовується t-критерий Стьюдента:
 ,
| (15) |
де: s2 – виправлена вибіркова дисперсія,
n1 – об’єм першої вибірки;
n2 – об’єм другої вибірки.
Інший варіант формули:
 ,
| (16) |
де: s2 – зміщена вибіркова дисперсія.
Розраховане за наведеними формулами емпіричне значення критерію Стьюдента зрівнюється з критичним значенням цього критерію. Критичне значення критерію Стьюдента вибирається з відповідної таблиці (див. Додаток Б) залежно від рівня значущості a (0,05; 0,01; 0,001) та кількості ступенів свободи f (f = n1 + n2 - 2).
Якщо емпіричне значення критерію Стьюдента не перевищує його критичного значення, то приймається нульова гіпотеза про відсутність статистично значимих відмінностей середніх арифметичних значень в двох вибірках. У протилежному випадку нульова гіпотеза відхиляється.
Для встановлення схожості-відмінності дисперсій в двох незалежних вибірках (які витягують з генеральних сукупностей, що мають нормальний розподіл) використовується критерій Фішера:
 ,
| (17) |
де: 
– більша дисперсія,
– менша дисперсія.
Розраховане за наведеною формулою емпіричне значення критерію Фішера зрівнюється з критичним значенням цього критерію. Критичне значення критерію Фішера вибирається з відповідної таблиці (див. Додаток В) залежно від рівня значимості a (0,05; 0,01; 0,001) і кількості ступенів свободи. Кількість ступенів свободи визначається окремо для чисельника та знаменника за формулами:
| f1 = n1 - 1, f2 = n2 - 1, | (18) |
де: n1 – об’єм вибірки з більшою дисперсією,
n2 – об’єм вибірки з меншою дисперсією.
Якщо емпіричне значення критерію Фішера не перевищує його критичного значення, то приймається нульова гіпотеза про відсутність статистично значимих відмінностей дисперсій в двох вибірках. У протилежному випадку нульова гіпотеза відхиляється.
Зауважимо що рівень значущості a характеризує ймовірність помилки відхилити істинну гіпотезу.
Приклад 2. У двох друкарських цехах були проведені заходи щодо підвищення якості продукції. У кожному цеху використовувалася своя методика підвищення якості. До проведення заходів в обох цехах мало місце однакове розсіювання (розкид) параметрів видання. Після проведення заходів в кожному цеху здійснені вибіркові дослідження формату видання, результати яких представлені в таблиці 4.
Визначити, чи дійсно методика, використана в 1 цеху, дала найбільше вирівнювання параметрів видань (взяти рівень значущості a=0,05).
Таблиця 4
Результати дослідження формату видання,
отримані в двох цехах
| Показник | 1 цех | 2 цех |
| кількість перевірених екземплярів видання | ||
| вибіркова дисперсія | 0,16 (мм) | 0,36 (мм) |
Для розв’язання цієї задачі розрахуємо емпіричне значення критерію Фішера:
F =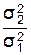 
= 0,36/0,16 = 2,25,
де: – дисперсія формату видання в 1 цеху,
– дисперсія формату видання в 2 цеху.
Кількість ступнів свободи:
f1=20,
f2=15.
Критичне значення критерію Фішера знайдемо по таблиці, наведеної в Додатку В (для a=0,05):
Fк= 2,203.
Оскільки F > Fк, то ми робимо висновок про наявність статистично значимих відмінностей дисперсій в 1 і 2 цеху. Отже, методика, використана в 1 цеху, оказала більший вплив на стабілізацію технологічного процесу.
