Ћабораторна робота 1
„ислов≥ характеристики статистичноњ виб≥рки
ћета роботи:
навчатис€ застосовувати виб≥рковий метод задл€ анал≥зу €кост≥ друкованих та мультимед≥йних видань
Ќавчальний матер≥ал
ћатематична статистика
ƒл€ контролю €кост≥ технолог≥чних процес≥в створенн€ друкованих та мультимед≥йних видань (насамперед, в пол≥граф≥њ) використовуютьс€ методи математичноњ статистики. ¬они Ї ефективним ≥нструментар≥Їм збору ≥ анал≥зу ≥нформац≥њ щодо €кост≥ виробничих операц≥й та готовоњ продукц≥њ.
ћатематична статистика вивчаЇ загальн≥ питанн€ анал≥зу масових к≥льк≥сних даних та маЇ справу звипадковими величинами (тобто з тими величинами, чињ значенн€ визначаютьс€ множиною чинник≥в випадкового характеру). —аме до таких Ц випадкових Ц величин в≥днос€тьс€ характеристики технолог≥чного процесу в пол≥граф≥њ.
2. ѕон€тт€ випадковоњ величини
¬ипадковою величиною називаЇтьс€ така зм≥нна величина, €ка приймаЇ те чи ≥нше значенн€ з де€коњ множини в залежност≥ в≥д випадку.
¬ид≥л€ють дискретн≥ та неперервн≥ випадков≥ величини.
ƒискретна випадкова величина Ц це випадкова величина, множина значень €коњ Ї ск≥нченою або зл≥ченною.
Ќеперервна випадкова величина приймаЇ своњ значенн€ з множини д≥йсних чисел.
3. «акон розпод≥лу дискретноњ випадковоњ ве≠личини
Ѕудь-€ка випадкова величина характеризуЇтьс€ своњм розпод≥лом, тобто описанн€м того, з €кою частотою зустр≥чаЇтьс€ кожне значенн€ випадковоњ величини.
ƒл€ повного описанн€ дискретноњ випадковоњ величини необх≥дно:
- вказати ус≥ њњ можлив≥ значенн€;
- задати ймов≥рн≥сть, з €кою приймаютьс€ ц≥ зна≠ченн€.
¬≥дпов≥дн≥сть м≥ж можливими значенн€ми дис≠кретних випадкових величин та њхн≥ми ймов≥рност€ми називаЇтьс€ законом розпод≥лу дискретноњ випадковоњ величини.
«ручно застосовувати табличний спос≥б описанн€ закону розпод≥лу дискретноњ випадковоњ величини: у першому р€дку таблиц≥ вказують значенн€ випадковоњ величини (хi, i=1, 2, 3Е), в другому р€дку Ц ймов≥рн≥сть цих зна≠чений (pi, i=1, 2, 3Е). “аку таблицю називають р€дом розпод≥лу дискрет≠ноњ випадковоњ величини (табл. 1).
“аблиц€ 1
–€д розпод≥лу дискрет≠ноњ випадковоњ величини
| ’ | х1 | х2 | Е | хi | Е |
| P | p1 | p2 | Е | pi | Е |
ќск≥льки дискретна випадкова величина обов'€зково прийме одне з≥ своњх значень хi, под≥њ {хi, i=1, 2, 3Е} утворюють повну групу под≥й, тобто виконуЇтьс€ умова:
 ,
,
де pi, Ц ймов≥рн≥сть того, що випадкова величина прийме значенн€ хi .
4. ‘ункц≥€ та щ≥льн≥сть розпод≥лу випадковоњ величини
–€д розпод≥лу Ц не ун≥версальна характеристика випадковоњ величини. ¬≥н ≥снуЇ т≥льки дл€ дискретних випадкових величин.
”н≥версальною характеристикою, €ка використовуЇтьс€ €к дл€ дискретних, так ≥ дл€ неперервних випадкових величин, Ї функц≥€ розпод≥лу.
‘ункц≥€ розпод≥лу випадковоњ величини визначаЇтьс€ формулою:
 ,
,
де: ’ Ц значенн€ випадковоњ величини,
х Ц д≥йсне число.
‘ункц≥€ розпод≥лу випадковоњ величини X описуЇ ймов≥рн≥сть того, що випадкова величина X набуде значень, менших заданого значенн€ х, де х Ц будь-€ке д≥йсне число.
|
|
|
¬ластивост≥ F(x):
1. «наченн€ F(x) належать в≥др≥зку [0, 1], тобто 0≤F(x)≤1.
2. F(x) Ц функц≥€, що не убуваЇ (тобто €кщо x1<x2, то F(x1)≤F(x2)).
ѕох≥дна в≥д функц≥њ розпод≥лу F(x) називаЇтьс€ щ≥льн≥стю розпод≥лу випадковоњ величини: f(x)= F'((x) (рис. 1-3).

–ис. 1. √раф≥ки функц≥њ розпод≥лу та щ≥льност≥ розпод≥лу випадковоњ величини, розпод≥леноњ за експоненц≥альним законом
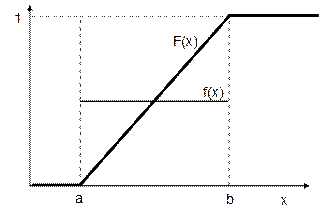
–ис. 2. √раф≥ки функц≥њ розпод≥лу та щ≥льност≥ розпод≥лу випадковоњ величини, €ка маЇ р≥вном≥рний розпод≥л

–ис. 3. √раф≥к щ≥льност≥ розпод≥лу випадковоњ величини, розпод≥леноњ за нормальним законом
5. „ислов≥ характеристики випадкових величин
„ислов≥ характеристики у стисл≥й форм≥ виражають ≥стотн≥ особливост≥ розпод≥лу випадковоњ величини. ќсновними характеристиками випадковоњ величини Ї њњ математичне спод≥ванн€ та дисперс≥€.
ћатематичним спод≥ванн€м дискретноњ випадковоњ величини ’, €ка задана своњм р€дом розпод≥лу (табл. 1), називаЇтьс€ число
 . .
| (1) |
ћатематичним спод≥ванн€м неперервноњ випадковоњ величини ’ називаЇтьс€ число
 . .
| (2) |
“аким чином, математичне спод≥ванн€ приблизно дор≥внюЇ середньому арифметичному ймов≥рних значень випадковоњ величини.
ƒисперс≥Їю випадковоњ величини ’ називаЇтьс€ математичне спод≥ванн€ квадрата в≥дхиленн€ випадковоњ величини ’ в≥д свого математичного спод≥ванн€:
 .
.
якщо випадкова величина X дискретна та задана своњм р€дом розпод≥лу, то
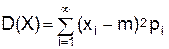 . .
| (3) |
якщо випадкова величина X неперервна та задана на в≥др≥зку [а, b], то
 . .
| (4) |
ƒисперс≥€ характеризуЇ м≥ру розс≥юванн€ значень випадковоњ величини ’ в≥дносно свого математичного спод≥ванн€.
–озм≥рн≥сть дисперс≥њ дор≥внюЇ квадрату розм≥рност≥ величини X. “ому дл€ ц≥лей анал≥зу часто використовують величину  , €ка називаЇтьс€ середн≥м квадратичним в≥дхиленн€м випадковоњ величини. ѓњ розм≥рн≥сть зб≥гаЇтьс€ з розм≥рн≥стю величини ’.
, €ка називаЇтьс€ середн≥м квадратичним в≥дхиленн€м випадковоњ величини. ѓњ розм≥рн≥сть зб≥гаЇтьс€ з розм≥рн≥стю величини ’.
6. ¬иб≥рковий метод в статистиц≥
«б≥р ≥нформац≥њ про технолог≥чний процес ≥ вироблену продукц≥ю зд≥йснюЇтьс€ шл€хом статистичного спостереженн€.
¬ид≥л€ють два р≥зновиди статистичного спостереженн€: суц≥льне та несуц≥льне. —уц≥льне спостереженн€ передбачаЇ досл≥дженн€ ознак ус≥х обТЇкт≥в загальноњ сукупност≥, що вивчаЇтьс€. ÷ей метод досл≥дженн€ пов'€заний ≥з значними трудовими ≥ матер≥альними витратами. ѕри несуц≥льному спостереженн≥ досл≥джують ознаки лише частини загальноњ сукупност≥ та, виход€чи з результат≥в досл≥дженн€, робл€ть висновки про властивост≥ ус≥Їњ сукупност≥ в ц≥лому.
” статистичн≥й практиц≥ найпоширен≥шим Ї виб≥ркове спостереженн€.
¬иб≥ркове спостереженн€ Ц це таке несуц≥льне спостереженн€, при €кому в≥дб≥р обТЇкт≥в, що п≥дл€гають обстеженню, зд≥йснюЇтьс€ у випадковому пор€дку, в≥д≥брана частина вивчаЇтьс€, а результати розповсюджуютьс€ на всю загальну сукупн≥сть обТЇкт≥в. —постереженн€ орган≥зовуЇтьс€ таким чином, що в≥д≥брана частина обТЇкт≥в репрезен≠туЇ в зменшеному масштаб≥ усю загальну сукупн≥сть.
—укупн≥сть обТЇкт≥в, з €коњ зд≥йснюЇтьс€ в≥дб≥р, називаЇтьс€ генеральною сукупн≥стю, ≥ вс≥ њњ узагальнен≥ показники називаютьс€ генеральними.
—укупн≥сть в≥д≥браних одиниць ≥менують виб≥рковою сукупн≥стю, ≥ вс≥ њњ узагальнен≥ показники називають виб≥рковими.
¬иб≥ркове спостереженн€ маЇ бути орган≥зоване й прове≠дено у в≥дпов≥дност≥ з науковими принципами теор≥њ виб≥ркового методу. ќсновними з таких принцип≥в Ї принцип забезпеченн€ випадковост≥ в≥дбору обТЇкт≥в та принцип достатност≥ њхньоњ к≥лькост≥. ƒотриманн€ цих принцип≥в дозвол€Ї отримати об'Їктивну гарант≥ю репре≠зентативност≥ виб≥рковоњ сукупност≥.
|
|
|
«адача виб≥ркового спостереженн€ пол€гаЇ в тому, щоб на основ≥ характеристик виб≥рковоњ сукупност≥ отримати достов≥рн≥ судженн€ про характеристики генеральноњ сукупност≥.
ѕро€в досл≥джуваноњ ознаки в генеральн≥й сукупност≥ Ї випадковою величиною (так, наприклад, випадковою величиною Ї ширина пол≥в в друкарському виданн≥). “ому основними характеристиками генеральноњ сукупност≥ Ї генеральне математичне спод≥ванн€ та генеральна дисперс≥€ досл≥джуваноњ ознаки.
ѕриблизн≥ значенн€ генерального математичного спод≥ванн€ та генеральноњ дисперс≥њ можна визначити за њхн≥ми виб≥рковими аналогами.
ƒл€ математичного спод≥ванн€ випадковоњ величини M(X) виб≥рковим аналогом Ї середнЇ арифметичне  спостережуваних значень випадковоњ величини:
спостережуваних значень випадковоњ величини:
 , ,  , ,
| (5) |
де: xi Ц значенн€ випадковоњ величини, спостережуване в i-тому досл≥д≥ (тобто результат i-го вим≥рюванн€ ознаки),
n Ц к≥льк≥сть досл≥д≥в (вим≥рювань).
÷ю характеристику називають виб≥рковим середн≥м випадковоњ величини.
«г≥дно з законом великих чисел, при необмеженому зб≥льшенн≥ к≥лькост≥ досл≥д≥в значенн€ виб≥ркового середнього наближаЇтьс€ до значенн€ генерального математичного спод≥ванн€. ѕри обмежен≥й к≥лькост≥ досл≥д≥в виб≥ркове середнЇ Ї випадковою величиною, €ка, проте, пов'€зана з генеральним математичним спод≥ванн€м ≥ може дати про нього де€ке у€вленн€.
¬иб≥рков≥ аналоги ≥снують дл€ вс≥х число≠вих характеристик випадкових величин. “ак, виб≥рковим аналогом генеральноњ дисперс≥њ Ї виб≥ркова дисперс≥€ S2, €ка розраховуЇтьс€ за формулою:
 , ,
| (6) |
де:  Ц виб≥ркове середнЇ,
Ц виб≥ркове середнЇ,
xi Ц значенн€ випадковоњ величини, спостережуване в i-тому досл≥д≥ (результат i-го вим≥рюванн€ ознаки),
n Ц к≥льк≥сть досл≥д≥в (вим≥рювань).
ѕоказник S, €кий дор≥внюЇ кореню з виб≥рковоњ дисперс≥њ, називаЇтьс€ виб≥рковим середньоквадратичним в≥дхиленн€м.
7. Ќезм≥щен≥ виб≥рков≥ характеристики
¬иб≥ркова характеристика називаЇтьс€ незм≥щеною, €кщо вона не м≥стить систематичноњ помилки, тобто середнЇ значенн€ виб≥рковоњ характеристики, €ке визначене при багатократному повторенн≥ виб≥рки об'Їмом n з одн≥Їњ й т≥Їњ ж генеральноњ сукупност≥, сходитьс€ до д≥йсного значенн€ в≥дпов≥дного генерального параметра.
¬иб≥ркове середнЇ Ї незм≥щеною оц≥нкою генерального середнього.
Ќезм≥щеною оц≥нкою генеральноњ дисперс≥њ Ї виправлена виб≥ркова дисперс≥€, що обчислюЇтьс€ за формулою:
 , ,
| (7) |
де: xi Ц значенн€ випадковоњ величини, спостережуване в i-тому досл≥д≥ (результат i-го вим≥рюванн€ ознаки),
 Ц виб≥ркове середнЇ,
Ц виб≥ркове середнЇ,
n Ц к≥льк≥сть досл≥д≥в (вим≥рювань).
“обто дл€ отриманн€ незм≥щеноњ оц≥нки виб≥ркову дисперс≥ю S2, отриману за формулою (6), треба помножити на величину n/(n - 1).
ѕоказник виправленоњ виб≥рковоњ дисперс≥њ використовуЇтьс€ при малому числ≥ спостережень (n<30). «азвичай вже при n>20 розб≥жн≥сть зм≥щеноњ та незм≥щеноњ оц≥нок стаЇ не≥стотною.






