Критерий Пирсона  2 (хи) является наиболее состоятельным при большом цикле наблюдений. Его состоятельность состоит в том, что он почти всегда опровергает неверную гипотезу и обеспечивает минимальную ошибку в принятии неверной гипотезы по сравнению с другими критериями. Этот критерий следует применять в тех случаях, когда теоретические значения параметров функции распределения случайной величины неизвестны.
2 (хи) является наиболее состоятельным при большом цикле наблюдений. Его состоятельность состоит в том, что он почти всегда опровергает неверную гипотезу и обеспечивает минимальную ошибку в принятии неверной гипотезы по сравнению с другими критериями. Этот критерий следует применять в тех случаях, когда теоретические значения параметров функции распределения случайной величины неизвестны.
Критерий согласия Пирсона  2 определяется по уравнению:
2 определяется по уравнению:

где  - число интервалов укрупненного статистического ряда;
- число интервалов укрупненного статистического ряда;
m, - опытная частота в i-ом интервале статистического ряда;
 - теоретическая частота в i-ом интервале.
- теоретическая частота в i-ом интервале.
Теоретическая частота:

где N- число точек информации;
F(t) и F( 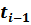 ) - интегральные функции i-го и (i - 1)-го интервалов статистического ряда.
) - интегральные функции i-го и (i - 1)-го интервалов статистического ряда.
Полученное значение  2 сравнивают с критическим (табличным) значением
2 сравнивают с критическим (табличным) значением  (r) этого критерия. Значение
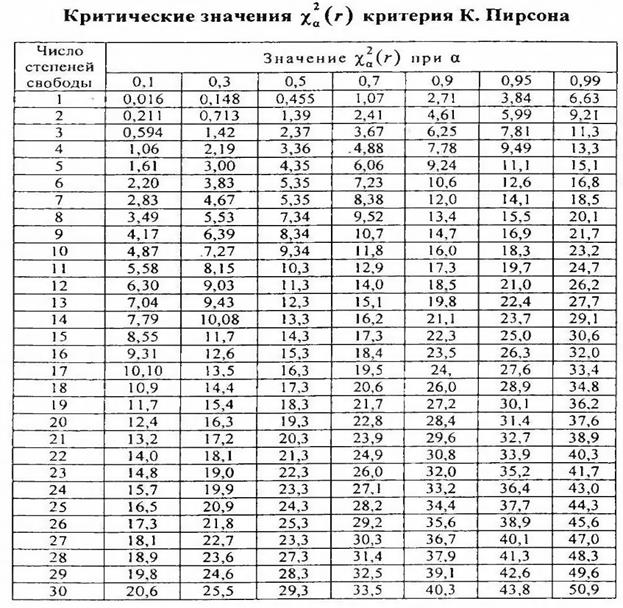
(r) этого критерия. Значение  (r) определяется по специальным математико-статистическим таблицам в зависимости от числа степеней свободы r, уровня значимости а или доверительной вероятности Р (см. табл.)
(r) определяется по специальным математико-статистическим таблицам в зависимости от числа степеней свободы r, уровня значимости а или доверительной вероятности Р (см. табл.)
Доверительной считается такая вероятность, которую можно признать достаточной для суждения о достоверности характеристик, полученных на основе выборочных наблюдений. В качестве доверительной вероятности принимают значения 0,95; 0,99; 0,999. Последняя обеспечивает более надежные выводы. Для инженерных расчетов приемлемой является доверительная вероятность Р = 0,95.
Число степеней свободы определяется по формуле:
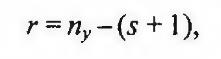
где s - количество параметров теоретического распределения (для нормального закона s = 1, для экспоненциального и распределения Вейбулла - s = 2).
 - число интервалов укрупненного статистического ряда;
- число интервалов укрупненного статистического ряда;
Гипотезу о предполагаемом законе распределения считают справедливой при условии  2 <
2 <  (r) Если
(r) Если  2 >=
2 >=  (r), то гипотезу отвергают.
(r), то гипотезу отвергают.
Недостатком критерия Пирсона  2 является то, что он не дает однозначной оценки для заключения об оптимальности принятого теоретического закона распределения. Кроме того, применение критерия
2 является то, что он не дает однозначной оценки для заключения об оптимальности принятого теоретического закона распределения. Кроме того, применение критерия  2 эффективно при числе результатов наблюдений N>30.
2 эффективно при числе результатов наблюдений N>30.






