При исследовании надежности машин и их элементов после предварительного анализа результатов наблюдений выдвигают предположение о виде закона распределения значений показателей надежности. Выбор закона распределения на начальном этапе можно осуществить с помощью вариационной сетки, представляющей собой изображение кумулятивной кривой (кумуляты) -вариационного ряда в системе координат, в которой на ось абсцисс наносится величина признака (случайная величина) в равномерном масштабе, а на ось ординат - кумулятивные частоты или вероятности в функциональном неравномерном масштабе, «вытягивающим» кумулятивную кривую в прямую линию.
Характер теоретического распределения показателей надежности можно установить по ряду косвенных признаков. Например, в том случае, когда определенные расчетным (экспериментальным) путем математическое ожидание и среднее квадратичное отклонение оказываются равными друг другу (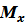 
=𝝈), следует воспользоваться показательным распределением. Используемое для описания редко встречающихся событий распределения Пуассона также имеет специфическое свойство ( 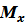=𝝈).
В случае соблюдения указанных условий принято считать фактическое распределение приблизительно подчиняющимся нормальному распределению.
Теоретический закон распределения для выравнивания опытной информации ориентировочно также устанавливают по величине коэффициента вариации V.
Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:
,
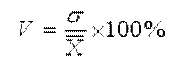где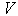 
- искомый показатель, 
- среднее квадратичное отклонение,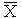 
- средняя величина.
При этом считается, что если V < 0,30, используют закон нормального распределения, если V> 0,50 закон распределения Вейбулла, если V= 1,0 -экспоненциальный. Если значение коэффициента вариации находиться в интервале 0,30...0,50, то выбирают тот закон распределения (закон нормального распределения или закон распределения Вейбулла), который лучше совпадает с распределением опытной информации.
Для окончательного выбора теоретического закона распределения используют критерии согласия. Под критерием согласия подразумевается совокупность условий, подтверждающих справедливость принятых гипотез.
Критерии согласия являются объективными оценками близости экспериментальных (опытных) и теоретических распределений показателей надежности. При этом статистические данные показателей по результатам эксплуатации машин также относятся к опытным.
Критерии согласия позволяют ответить на вопрос: вызвано ли расхождение опытного и теоретического распределений случайными причинами, связанными с недостаточным числом наблюдений или существенными причинами, т.е. тем, что теоретическое распределение плохо воспроизводит фактическое. При этом критерий согласия обычно выступает в виде некоторой величины, оцениваемой с определенной вероятностью.
Разработанные в настоящее время методы исследования надежности в большинстве случаев требуют аналитического описания зависимостей уровня надежности элементов и систем от времени, для чего необходимо описание статистических распределений (сглаживание или выравнивание статистических данных) различного рода математическими функциями и, в первую очередь, теоретическими законами распределения f(x). При этом необходимо так выбрать аппроксимирующую функцию f (х), чтобы она учитывала вероятностные отклонения случайных точек (f*(x), х), получаемых при проведении испытаний, и согласовалось с данными испытаний, т.е. чтобы можно было считать справедливым равенство:
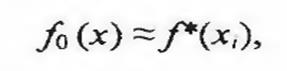
где f *(х,) - статистическая плотность распределения случайной величины.
Для количественной оценки выполнения равенства разработано несколько критериев согласия. Суть их сводиться к тому, что выбирается некоторый количественный показатель ∆ меры расхождения между выбранной функцией теоретического распределения и результатом статистического эксперимента. Задается такое допустимое ∆д, что, если полученная в результате опыта мера расхождения ∆оп окажется меньше, чем ∆д, то принимается гипотеза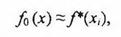 
.
В качестве меры расхождения ∆ обычно берут определенным образом выбранную функцию от разности между f*(t) и fo(t), либо разность между теоретической и статистической функцией распределения. Так как величина ∆ является функцией от случайных величин f (x) то она также является случайной величиной, плотность распределения которой 𝝋(∆) зависит от способа выбора меры ∆ и объема статистических данных N.
При обработке информации по показателям надежности техники используют несколько критериев, различных по мощности и методу обработки исходных данных. Наиболее часто в качестве критериев согласия опытных и теоретических распределений показателей надежности применяются следующие критерии: Колмогорова, Пирсона х2 (хи -квадрат), Романовского и Мизеса.
