Для оценки безотказности изделий используют следующие показатели:
P(t) - вероятность безотказной работы за время t;
Q(t)- вероятность отказа;
Tср - средняя наработка до первого отказа (или среднее время безотказной работы);
Tо - средняя наработка на отказ;
T - средняя наработка между отказами;
λ(t) - интенсивность отказов;
λ1(t) - параметр потока отказов — для восстанавливаемых изделий;
ω(t) - средняя частота отказов.
Кроме вышеперечисленных, могут использоваться и другие критерии, оценивающие тот или иной фактор в зависимости от особенных условий работы изделия.
Показатели безотказности могут вводиться как по отношению ко всем возможным отказам изделия, так и по отношению к какому-либо одному типу отказа.
Очевидно, что изделие работает безотказно, если оно при этом сохраняет свои рабочие параметры в установленных пределах в течение рассматриваемого промежутка времени (t).
Вероятность безотказной работы отдельного изделия оценивается как:
P(t) = P (T≥t), (5.1)
где T— время от начала работы до отказа;
t— время, для которого определяется вероятность безотказной работы.
Величина Тможет быть больше, меньше или равна t. Следовательно, 0 ≤ P(t) ≤ 1
Вероятность безотказной работы - это статистический и относительный показатель сохранения работоспособности однотипных изделий серийного производства, выражающий вероятность того, что в пределах заданной наработки отказ изделий не наступает. Для установления значения вероятности безотказной работы серийных изделий используют формулу для среднестатистического значения.
, (5.2)
где N — число наблюдаемых изделий (или элементов);
N 0 — число отказавших изделий за время t;
N p — число работоспособных изделий к концу времени t испытаний или эксплуатации.
Вероятность безотказной работы является одной из наиболее значимых характеристик надежности изделия, так как она охватывает все факторы, влияющие на надежность. Для вычисления вероятности безотказной работы используются данные, накапливаемые путем наблюдений за работой при эксплуатации или при специальных испытаниях. Чем больше изделий подвергается наблюдениям или испытаниям на надежность, тем точнее определяется вероятность безотказной работы других однотипных изделий. Так как безотказная работа и отказ - взаимно противоположные события, то оценку вероятности отказа (Q (t)) определяют по формуле:
. (5.3)
Распределение отказов во времени характеризуется функцией плотности распределения f(t) наработки до отказа. Статистическая оценка плотности распределения имеет вид:
,
где Δ N (t) - приращение числа отказавших изделий за время Δt.
Распределение отказов во времени характеризуется функцией плотности распределения f(t) наработки до отказа. Статистическая оценка плотности распределения имеет вид:
,
где Δ N (t) - приращение числа отказавших изделий за время Δt.
В вероятностном смысле плотность распределения наработки до отказа:
Вероятности отказов и безотказной работы в функции плотности распределения наработки на отказ выражаются зависимостями:
; (5.4)
;
Типичная зависимость Р (t) от t приведена на рисунке 2.
 |
Рисунок 2-- Типичное изменение вероятности безотказной работыт изделия во времени.
Относительная безотказность Р(t), определенная на основе экспериментальных данных, является отправной характеристикой для проектирования новой аналогичной техники с повышенной надежностью.
При проектировании оценивают возможное значение Р(t) будущего изделия методом расчета. Повышается Р(t) oт использования более надежных деталей и элементов (блоков, частей), от повышения надежности методов работы техники, от оптимизации структурных схем изделии, а также от использования технически более эффективных технологии изготовлении новых образцов техники.
Расчет среднестатистического времени наработки до отказа (или среднего времени безотказной работы) по результатам наблюдений определяют по формуле: 
, (5.5)
где N - число элементов или изделий, подвергнутых наблюдениям или испытаниям;
t - время безотказной работы i -го элемента (изделия).
Средняя наработка до отказа - это математическое ожидание наработки изделия до первого отказа. Следовательно, среднюю наработку до отказа можно определять, по формулам:
-для непрерывной функции распределения надежности
;
-для дискретной функции надежности
, (5.6) где Р (ti) = 
.
В последних формулах Np - число работоспособных изделии на интервале наработки ti+1 – ti; N -общее число объектов, поставленных на испытание или в эксплуатацию; Δ t = ti+1 – ti; k - общее число рассматриваемых интервалов наработки эмпирической функции надежности.
Средняя наработка на отказ - это отношение наработки восстанавливаемого изделия к математическому ожиданию числа его отказов в течение этой наработки.
Статистическую оценку среднего значения наработки на отказ вычисляют как отношение суммарной наработки за рассматриваемый период испытаний или эксплуатации изделий к суммарному числу отказов этих изделий за тот же период времени:
, (5.7)
Показатель наработки на отказ можно оптимизировать по экономическим критериям. На рисунке 3 показаны принципиальные зависимости затрат: Зо — затраты па повышение времени наработки на отказ; 3э — затраты эксплуатационные; Зс — суммарные затраты.
 |
Рисунок 3 – Общая модель экономически обоснованных норм
показателя надежности Tо.
Средняя наработка между отказами - это математическое ожидание наработки изделия от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа.
Статистическую оценку среднего значения наработки между отказами вычисляют как отношение суммарной наработки изделия между отказами за рассматриваемый период испытаний или эксплуатации к числу отказов этого (их) объекта(ов) за тот же период:
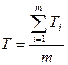, (5.8)
где т — число отказов за время t.
Интенсивность отказов λ(t) характеризует условную плотность вероятности возникновения отказов невосстанавливаемого изделия за рассматриваемый период времени в случае, если до этого их не наблюдалось 
. (5.9)
На практике при установлении статистическою значения интенсивности отказов λс (t) пользуются формулой:
, (5.10)
где N 0(Δ t) - число отказавших изделий в интервал времени Δ t;
N ср - среднее число исправно работавших изделий в интервале Δ t. Очевидно, что 
,
где Ni, Ni+1 - число исправно работающих изделий соответственно в начале и конце интервала Δ t.
Интенсивность отказов λ(t) показывает, какая часть изделий становится неисправной за единицу времени работы по отношению к среднему числу исправно работающих изделий.
Интенсивность отказов используется в качестве одного из основных критериев при оценке надежности изделий.
На рисунке 4 показано характерное изменение интенсивности отказов во времени для большинства промышленных изделий. На рисунке отмечено три периода: 1 — приработка, 2 — устойчивая работа, 3 — ускоренное старение и износ.
 |
Рисунок 4--Изменение интенсивности отказовво времени эксплуатации
Вероятность безотказной работы, выраженная через интенсивность отказов, имеет вид:
.
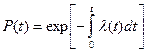Это уравнение является одним из основных в теории и практике расчетов показателей надежности.
Параметр потока отказов λI(t) для восстанавливаемого изделия характеризует плотность вероятности появления отказа ремонтопригодного объекта для определенного момента времени
,
где f (t)- плотность распределения потока отказов за период времени t.
