Покажем, как можно прийти к её формулировке. Пусть поле создано бесконечно длинным проводником с током. Линии напряженности в этом случае представляют собой окружность. Вычислим циркуляцию напряженности по окружности произвольного радиуса.
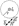
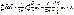
Данное выражение получено для простой геометрии. Однако оно справедливо для любой геометрии. Поэтому возводится в ранг закона и называется теоремой о циркуляции.
Закон: Циркуляция напряженности магнитного поля по произвольному замкнутому контуру равна току, охваченному этим контуром.
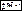
– в интегральной форме.
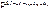
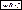
– в дифференциальной форме.
Так как циркуляция не равна нулю, то магнитное поле носит вихревой характер. Линии напряженности магнитного поля замкнуты.
Поле цилиндрического проводника с током.
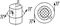
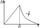Внутри: 
