Основные понятия алгебры логики
| О |
снову любого дискретного вычислительного устройства составляют элементарные логические схемы, работа которых базируется на законах и правилах алгебры логики.
Алгебра логики (булева алгебра) – раздел дискретной математики, изучающий высказывания и логические операции над ними.
Высказывание – связное повествовательное предложение, о котором можно сказать, истинно оно или ложно. Высказывание не содержит внутреннего противоречия и несет смысловую нагрузку. Каждое составное высказывание можно выразить в виде логической формулы (выражения), в которую входят логические переменные, обозначающие высказывания, и логические операции.
Основными, или базовыми, операциями булевой алгебры являются: НЕ (NOT), ИЛИ (OR) и И (AND).
Операция НЕ называется логическим отрицанием, или инверсией, и обозначается знаком (—, Ø). Результат операции логического отрицания равен 1, если значение переменной равно 0 и, наоборот, равна 0, если переменная равна 1.
Операция ИЛИ называется логическим сложением, или дизъюнкцией, и обозначается знаком сложения (+, Ú). Дизъюнкция двух переменных равна 1, если хотя бы одна переменная равна 1 и равна 0, если обе переменные равны 0.
Операция И называется логическим умножением, или конъюнкцией, и обозначается знаком умножения (×, Ù, &). Конъюнкция двух переменных равна 0, если хотя бы одна переменная равна 0 и равна 1, если обе переменные равны 1.
Таблица истинности – табличное представление логической операции, в котором перечислены все возможные сочетания логических значений операндов вместе со значением результата операции для каждого из этих сочетаний. Для указанных выше операций таблицы истинности имеют следующий вид.
| Инверсия | Дизъюнкция | Конъюнкция | |||||||
| A | Ø A | A | B | A Ú B | A | B | A & B | ||
В алгебре логики кроме базовых логических операций используются и другие операции, например импликация и эквивалентность.
Операция импликации (логическое следование) образуется соединением двух переменных с помощью связки «если…то» и обозначается знаком (®). Импликация принимает значение 0 тогда и только тогда, когда первая переменная имеет значение 1, а вторая – 0. Это означает, что составное высказывание ложно только тогда, когда из истинной предпосылки (первое высказывание) вытекает ложный вывод (второе высказывание). Например, высказывание «Если число делится на 10, то оно делится на 3» принимает значение ложь, так как из истинной предпосылки «число делится на 10» делается ложный вывод «оно делится на 3».
Операция эквивалентности (логическое равенство) образуется соединением двух переменных с помощью связки «…тогда и только тогда, когда…» и обозначается знаком (~). Результат операции эквивалентности равен 1 тогда и только тогда, когда обе переменные одновременно имеют значение либо 0 либо 1. Это означает, что составное высказывание истинно, когда входящие в него высказывания одновременно либо истинны либо ложны. Например, высказывание «Компьютер может производить вычисления тогда и только тогда, когда он включен» принимает значение истины, так как оба высказывания «Компьютер может производить вычисления» и «когда он включен» являются истинными.
Таблицы истинности для операций импликации и эквивалентности имеют следующий вид.
| Импликация | Эквивалентность | |||||
| A | B | A ® B | A | B | A ~ B | |
Для преобразования логических формул с целью их упрощения используются законы алгебры логики: законыоднопарных элементов, законы отрицания и комбинационные законы.
Законы однопарных элементов: а) универсального множества: x +1=1; x ×1= x; б) нулевого множества: x +0= x; x ×0=0.
Законы отрицания: а) двойного отрицания:  = x; б) дополнительности: x +
= x; б) дополнительности: x +  =1; x
=1; x  =0; в) двойственности (правило де Моргана):
=0; в) двойственности (правило де Моргана):  ;
;  .
.
Комбинационные законы:
а) тавтологии: x + x = x; x × x = x;
б) коммутативные: x 1+ x 2= x 2+ x 1; x 1× x 2= x 2× x 1;
в) ассоциативные (сочетательные): x 1+(x 2+ x 3)=(x 1+ x 2)+ x 3; x 1(x 2 x 3)=(x 1 x 2) x 3;
г) дистрибутивные (распределительные): x 1(x 2+ x 3)= x 1 x 2+ x 1 x 3; x 1+ x 2 x 3=(x 1+ x 2)(x 1+ x 3);
д) закон абсорбции (поглощения): x 1+ x 1 x 2= x 1; x 1(x 1+ x 2)= x 1;
е) склеивания:  ;
;  .
.
Логической функцией (булевой, двоичной)называется логическая (двоичная) переменная y, значение которой зависит от значений двоичных переменных (x 1, x 2, …, xn), являющихся аргументами: y = y (x 1, x 2, …, xn). Любое составное высказывание можно рассматривать как логическую функцию y (x 1, x 2, …, xn), аргументами которой являются простые высказывания (логические переменные x 1, x 2, …, xn). Задание логической функции означает, что каждому из возможных сочетаний аргументов соответствует определенное значение функции y. Если число аргументов равно n, то количество возможных сочетаний определяется как 2 n. Для каждой логической функции можно построить таблицу истинности, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов.
В алгебре логики все логические операции путем логических преобразований могут быть сведены к трем базовым: логическому умножению, логическому сложению и логическому отрицанию. Приоритеты выполнения логических операций в логических функциях следующие: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. Рассмотрим на примерах приемы и способы упрощения логических формул и составления таблиц истинности для логических функций.
Пример 1. Используя законы алгебры логики, упростить логические формулы.
а)  . При преобразовании законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, законы дополнительности и нулевого множества.
. При преобразовании законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, законы дополнительности и нулевого множества.
б)  . Применяется правило де Моргана; общий множитель выносится за скобки; используется закон дополнительности.
. Применяется правило де Моргана; общий множитель выносится за скобки; используется закон дополнительности.
в)  . Общие множители выносятся за скобки; применяется закон универсального множества.
. Общие множители выносятся за скобки; применяется закон универсального множества.
Пример 2. Преобразовать логическую функцию  . В этом примере для обозначения дизъюнкции и конъюнкции используются знаки Ú и &.
. В этом примере для обозначения дизъюнкции и конъюнкции используются знаки Ú и &.
Решение
 .
.
Пример 3. При каких значениях переменных A и B логическая функция  принимает значение, равное 0.
принимает значение, равное 0.
Решение
Составим таблицу истинности для заданной логической функции.
| A | B | 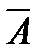
|  & B & B
| A & B | 
|  & B Ú & B Ú 
|
Из таблицы видно, что логическая функция F принимает значение 0 только при A =1 и B =1.
Логические основы ЭВМ
| Л |
юбое вычислительное устройство компьютера (например, двоичный сумматор) представляет собой электронную логическую схему, состоящую из логических элементов.
Логический элемент (простой функциональный узел)– это простая электронная схема, которая реализует элементарную логическую функцию. К базовым логическим элементам относятся электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ, а также триггер. На входы логического элемента поступают сигналы – значения аргументов, на выходе появляется сигнал – значение функции. Входные и выходные сигналы логических элементов могут иметь одно из двух логических состояний: 1 (истина) или 0 (ложь). Работу логического элемента (преобразование сигналов) описывают с помощью таблицы истинности (состояния), соответствующей определенной логической функции.
Схема И реализует конъюнкцию двух или более логических значений. Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Условное графическое изображение логического элемента представлено на рисунке
| y=x 1 x 2 |
| x 2 |
| x 1 |
| & |
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Единица на выходе схемы ИЛИ будет тогда и только тогда, когда на любом из входов будет единица. Условное графическое изображение логического элемента представлено на рисунке.
| y=x 1Ú x 2 |
| x 2 |
| x 1 |
Схема НЕ (инвертор) реализует операцию логического отрицания. Единица на выходе схемы НЕ будет тогда, когда на входе будет ноль. Когда на входе единица, то на выходе будет ноль. Условное графическое изображение логического элемента представлено на рисунке.
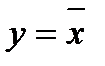
|
| x |
Схема И-НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Условное графическое изображение логического элемента и таблица истинности представлены ниже.
| x 1 | x 2 | 
|

|
| x 1 |
| & |
| x 2 |
| x 1 | x 2 | 
|
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Условное графическое изображение логического элемента и таблица истинности представлены ниже.

|
| x 1 |
| x 2 |
Триггер – электронное устройство с двумя устойчивыми состояниями, предназначенное для хранения 1 бита данных. Триггер является важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop («хлопанье»). Самый распространенный тип триггера – RS- триггер. Он содержит защелку из двух элементов ИЛИ - НЕ и два раздельных статических входа управления: вход R (сброс – reset) и вход S (установка – set). Для RS- триггера с прямыми входами, когда за активный уровень принят уровень логической единицы, принципиальная схема и таблица истинности имеют следующий вид.
| Вход | Выходы | ||
| R | S | Q | 
|
| Без изменений | |||
| Не определено |

|
| Q |
| S |
| R |
Режим работы триггера, при котором R =1, а S =0, называется режимом очистки, при R =0, S =1 – режимом записи, а при R =0, S =0 – режимом хранения. Комбинация R =1, S =1 является запрещенной, так как на выходе Q может установиться состояние, как логического ноля, так и логической единицы. Рассмотрим пример построения электронной схемы, состоящей из базовых логических элементов.
Пример. Одноразрядный двоичный сумматор имеет два входа (x 1 и x 2) и два выхода (S – сумма и P – перенос в старший разряд). Таблица истинности для сумматора имеет следующий вид.
| Входы | Выходы | ||
| x 1 | x 2 | S=f 1 (x 1, x 2) | P = f 2 (x 1, x 2) |
Записать логические функции для S и P и составить электронную логическую схему сумматора, используя основные логические элементы.
Решение
Выходные функции S и P можно представить следующим образом:  ; P = f 2 (x 1, x 2)= x 1 x 2.
; P = f 2 (x 1, x 2)= x 1 x 2.
Тогда структурная схема сумматора будет иметь следующий вид.
| P |
| S |
| x 1 |
| & |
| & |
| & |
| x 2 |

Тесты
| № п/п | Вопрос | Варианты ответов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Данной схеме соответствует логическая функция...

| 1.  2.
2. 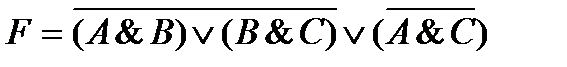 3.
3. 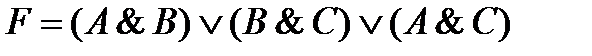 4.
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Какое из следующих предложений является высказыванием? | 1. Ура, скоро Новый год! 2. Светает. 3. 3+4*56. 4. Первый зимний месяц – декабрь. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Истинность двух высказываний: «Миша посмотрит фильм А, но не посмотрит фильм С» и «Из двух фильмов В и C Миша посмотрит только один» означает просмотр фильмов… | 1. А, В 2. В 3. А, В, С 4. В, С 5. А, С | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Среди указанных предложений ложным высказыванием будет... | 1. Который час? 2. Это утверждение не может быть истинным. 3. 10 не делится на 2, и 5 больше 3. 4. Площадь отрезка меньше длины куба. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| При вычислении логических выражений логические операции: 1 – дизъюнкция; 2 – инверсия; 3 – конъюнкция выполняются в соответствии с приоритетом... | 1. 3-2-1 2. 1-2-3 3. 2-1-3 4. 2-3-1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Из предложенных высказываний выберите логическое произведение. | 1. За завтраком я выпиваю чашку кофе или чая. 2. Без труда не выловишь и рыбку из пруда. 3. На столе в беспорядке лежали книжки и тетрадки. 4. Числа, кратные 4, кратны 2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Из предложенных высказываний выберите логическую сумму. | 1. Хорошо, когда утро начинается с зарядки и обливания холодной водой. 2. В салат можно положить или консервированные овощи, или сырые, или те и другие. 3. В холодный и пасмурный день хорошо сидеть дома. 4. Мне предложили купить билеты в театр: или в партер, или в бельэтаж. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Из нижеприведенных фраз выберите ту, которая является истинным высказыванием. | 1. Все кошки серы. 2. Познай самого себя. 3. Талант всегда пробьет себе дорогу. 4. Число 7 –простое. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На рисунке приведена таблица истинности для выражения, содержащего две логические операции. Одна из них – A Ú B (второй столбец).
В заголовке третьего столбца таблицы должно быть указано логическое выражение… | 1. (A Ú B)& C
2.  3. (A Ú B)Ú C
4.
3. (A Ú B)Ú C
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Символом F обозначено логическая функция от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности функции F.
Логической функции F соответствует логическое выражение…
| 1. 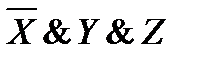 2.
2.  3.
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Имеются две логические переменные: A и B. Упростите логическое выражение F, составленное из этих переменных: F =(A Ù B)Ú(Ø A ÚØ B) | Введите ответ:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Имеются две логические переменные: A и B. Составьте и упростите логическое выражение F, соответствующее следующей таблице истинности:
| Введите ответ:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На рисунке представлено условное графическое изображение логической схемы. Связь между выходом Z и входами X и Y для данной логической схемы записывается в виде …
| 1. Z = X & Y
2. Z = X Ú Y
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На входе логической схемы для F =1 возможна следующая комбинация сигналов (А, В, С, D)…
| 1. (1 1 0 0) 2. (1 1 1 0) 3. (1 0 1 0) 4. (0 1 1 0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Логическому выражению 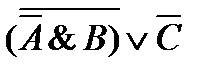 равносильно выражение … равносильно выражение …
| 1.  2.
2.  3.
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Логическое выражение НЕ((Y >4) ИЛИ (Y <1)) И (Y =2) истинно, когда значение переменной Y равно … | 1. 1 2. 2 3. 0 4. 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблицей истинности для операции логического умножения является… | 1. 2.
3. 4.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На рисунке приведена таблица истинности для выражения, содержащего две логические операции. Одна из них – A Ú B (второй столбец).
В заголовке третьего столбца таблицы должно быть указано логическое выражение… | 1. (A Ú B)Ù C 2. Ø(A Ú B) 3. (A Ú B)Ù(C ÚØ C) 4. (A Ú B)Ú C | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Применяя побитовую операцию AND к числам 111112 и 101012, получим двоичный код десятичного числа... | 1. 31 2. 32 3. 21 4. 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На рисунке представлено условное обозначение логического элемента…
| 1. ИЛИ 2. И 3. НЕ 4. ИЛИ - НЕ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Логический элемент по ГОСТ обозначается следующим образом:
Какая логическая операция ему соответствует? | 1. Дизъюнкция. 2. Отрицание. 3. Конъюнкция. 4. Эквивалентность. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Логический элемент по ГОСТ обозначается следующим образом:
На выходе схемы будет 1 (истина), если… | 1. X =1 или Y =1 2. X =1 и Y =1 3. X =1 или Y =0 4. X =0 или Y =1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблице истинности
соответствует логическое выражение… | 1. F = not X and not Y 2. F = not X or not Y 3. F = not X xor Y 4. F = X and Y or not Y 5. F = X or Y and not X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Логическое выражение (x <= 5) and not ((x = 3) or (x > 5)) принимает значение True при следующих значениях переменной x. | 1. 4 2. 3 3. 6 4. 5 5. 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Функциональной схеме
соответствует логическая функция… | 1.  2.
2.  3.
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В какой строке таблицы истинности допущена ошибка?
| 1. 1 2. 2 3. 3 4. 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Имеются логические переменные A, B и F, связанные таблицей истинности следующим образом:
Какова зависимость F от A и B? | 1. От A не зависит, F = Ø B. 2. От A не зависит, F = B. 3. F не зависит от A и B. 4. F зависит от A и B, F = A Ù B. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дана таблица истинности:
Какой логической операции она соответствует? | 1. Дизъюнкция 2. Отрицание 3. Конъюнкция 4. Эквивалентность | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дана таблица истинности:
Какому логическому выражению она соответствует? | 1. Ø X ÙØ Y 2. Ø Y 3. Ø X 4. Ø X ÚØ Y | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Представленный на рисунке логический элемент
выполняет операцию... | 1. ИЛИ-НЕ 2. И-НЕ 3. НИ-НИ 4. ИЛИ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Верны ли следующие логические выражения? а). Если высказывания A и B ложны, то импликация A ® B тоже ложна. б). Если высказывания A и B истинны, то импликация A ® B тоже истинна. | 1. Верно только первое выражение. 2. Верны оба выражения. 3. Оба выражения неверны. 4. Верно только второе выражение. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Имеются три логические переменные A, B и С, из которых составлено логическое выражение: F =(A Ù B ÙØ С)Ú(Ø A Ù B ÙØ С)Ú(B Ù С) Упростите логическое выражение F и определите, значения каких переменных влияют на значение F? | 1. A и B 2. B 3. C 4. B и C | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Имеются три логические переменные: A, B и C. При помощи логических операций конъюнкции, дизъюнкции и отрицания напишите логическое выражение F, соответствующее следующей таблице истинности, и упростите его.
| Введите ответ:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Имеются три логические переменные A, B и С, из которых составлено логическое выражение: F =(Ø A ÙØ B ÙØ С)Ú(Ø A Ù B ÙØ С)Ú А Ú С Упростите логическое выражение F и определите, значения каких переменных не оказывают влиянияна значение упрощенного выражения F? | 1. Значения ни одной из переменных не влияет на значение F. 2. A 3. B и C 4. C | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определите, какая из представленных формул соответствует высказыванию: «Если в числе сумма цифр, стоящих на четных местах, равна сумме цифр, стоящих на нечетных местах, то число делится на 11»? | 1. (A Ú B)Ú C 2. (A Ú B)® С 3. (A & B)& C 4. A ® B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В таблице истинности указаны значения трех логических переменных: A, B и C. Заполните
| Введите ответ:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На один вход логической схемы подается сигнал А, который может принимать значение 1 (истина) или 0 (ложь), на другой вход подается 1 (истина).
Как зависит значение F на выходе схемы от входного сигнала А? | 1. F = A 2. Не зависит от A, всегда 1 (истина). 3. Не зависит от A, всегда 0 (ложь). 4. F =Ø A | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дана логическая схема.
При каких значениях входных переменных X и Y на выходе схемы F будет иметь значение 1 (истины)? | 1. 0 и 0 2. 0 и 1 3. 1 и 0 4. 1 и 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На оба входа логической схемы подается сигнал А, который может принимать значение 1 (истина) или 0 (ложь).
Какое значение F будет на выходе схемы? | 1. Всегда 1 (истина). 2. A 3. Ø A 4. Всегда 0 (ложь). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На один вход логической схемы И подается сигнал А, который может принимать значении 1 (истина) или 0 (ложь), на другой вход – его отрицание Ø A.
Какое значение F будет на выходе схемы? | 1. A 2. Всегда 1 (истина) 3. Всегда 0 (ложь). 4. Ø A | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Запишите формулу, отражающую логическое преобразование, выполняемое схемой.
| 1. Y = X 1Ù X 2Ú X 3
2.  3.
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| К понятиям формальной логики не относится... | 1. Истинность. 2. Эквивалентность. 3. Абстрагирование. 4. Высказывание. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Среди перечисленных предложений высказыванием является... | 1. ” x <2, x € R ” (Вещественное число x меньше двух). 2. Площадь отрезка меньше длины куба. 3. Юпитер – ближайшая к Солнцу планета. 4. Берегись автомобиля! | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Для запоминания 2 байт информации достаточно ___ триггера(ов). | 1. 2 2. 16 3. 8 4. 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Из заданных логических выражений тождественно истинным является … | 1. А И НЕ А ИЛИ НЕ А 2. А ИЛИ НЕ В ИЛИ НЕ А 3. А И НЕ А ИЛИ В 4. А И НЕ В ИЛИ А | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Электронная схема, запоминающая 1 бит информации, – это … | 1. Транзистор. 2. Сумматор. 3. Конъюнктор. 4. Триггер. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Укажите последовательность логических операций в порядке убывания их приоритетов. | 1. Инверсия, дизъюнкция, конъюнкция, импликация. 2. Инверсия, конъюнкция, дизъюнкция, импликация. 3. Импликация, конъюнкция, дизъюнкция, инверсия. 4. Импликация, дизъюнкция, конъюнкция, инверсия. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На рисунке представлено условное графическое изображение логической схемы. Связь между выходом Z и входами X и Y для данной логической схемы записывается в виде …
| 1. Z = X Ù Y
2. Z = X Ú Y
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Электронное устройство, схема которого представлена на рисунке, называется …
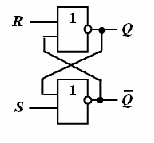
| 1. Триггером. 2. Реле. 3. Транзистором. 4. Сумматором. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Для того чтобы логическое выражение (X & Ø X)? (Y & Ø Y) было тождественно истинным, вместо знака? в нем … | 1. Нельзя поставить ни знак дизъюнкции (Ù), ни знак конъюнкции (&). 2. Можно поставить знак дизъюнкции (Ù), но не знак конъюнкции (&). 3. Нельзя поставить знак дизъюнкции (Ù), но можно поставить знак конъюнкции (&). 4. Можно поставить как знак дизъюнкции (Ù), так и знак конъюнкции (&). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Логическая функция  принимает значение Ложь (0) при … принимает значение Ложь (0) при …
| 1. A =1; B =0 2. A= 0; B= 0 3. A =0; B =1 4. A =1; B =1 |






