Сформулировь закон взаимосвязи массы и энергии. Что такое масса покоя; энергия покоя?

Взаимосвязь массы и энергии покоя

Масса тела и его энергия покоя связаны соотношением

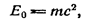
из которого вытекает, что всякое изменение массы тела Δm сопровождается изменением энергии покоя ΔЕ_о, причем эти изменения пропорциональны друг другу;

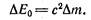
Это утверждение носит название закона взаимосвязи массы и энергии покоя (иногда для

краткости говорят просто об энергии).

Взаимосвязь m и Ео приводит к тому, что суммарная масса взаимодействующих частиц не сохраняется

Убедимся в этом на следующем примере. Пусть две одинаковые частицы массы m, движущиеся с равными по модулю и противоположно направленными скоростями, претерпевают абсолютно неупругое соударение, в результате которого образуется новая неподвижная частица. До соударения полная энергия каждой частицы равна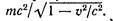

Полная энергия образовавшейся частицы равна Мс², где М — масса новой частицы. Из закона сохранения энергии cледует, что 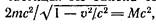откуда

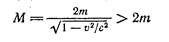
Таким образом,, масса образовавшейся частицы

больше суммы масс исходных частиц. Это обусловлено тем, что кинетическая энергия частиц превратилась в эквивалентное количество энергии покоя, а это в свою очередь привело к возрастанию массы на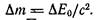

При распаде неподвижной частицы на несколько разлетающихся в разные стороны частиц наблюдается обратное явление — сумма масс образовавшихся частиц оказывается меньше массы исходной частицы на величину, равную суммарной кинетической энергии этих частиц, деленной на с².

В основе работы атомных электростанций лежит цепная реакция деления ядер урана. Суммарная масса образовавшихся при делении осколков (ядер более легких атомов) меньше массы ядра урана. Поэтому процесс деления сопровождается уменьшением энергии покоя частиц. Разность энергий покоя превращается в кинетическую энергию осколков и в энергию возникающего при делении электромагнитного

излучения.

Рассмотрим тело, состоящее из N частиц с массами m₁, m₂,..., m_N. Тело не будет распадаться на образующие его частицы при условии, что они связаны друг с другом. Эту связь можно охарактеризовать энергией E_св, которую нужно затратить, чтобы разорвать связь между частицами и разнести их на такие расстояния, при которых взаимодействием частиц друг с другом можно пренебречь. Энергию Есв называют энергией связи системы частиц.

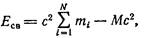
где М — масса системы (масса тела).'

Из формулы E2.3) следует, что энергия связи будет положительной в том случае, когда масса тела М меньше суммы масс образующих тело частиц.

При слиянии частиц высвобождается энергия Есв '(например, в виде электромагнитного излучения). Чтобы разделить тело на частицы, из которых оно состоит, нужно затратить энергию Есв.

Примером может служить атомное ядро. Так, ядро урана-238 имеет массу М = 395,2-10~27 кг. Оно состоит из 92 протонов с массой m_p = 1,6727-10~27 кг и 146 нейтронов с массой m_n= 1,6750-10 27 кг. Подстановка значений масс в формулу дает для энергии связи протонов и нейтронов в ядре урана-238 значение

 

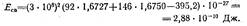
6.Показать, что (Е²–р²с²) является инвариантом.

Из двух возможных в ньютоновской механике

формулировок второго закона Ньютона в релятивистской механике справедлива только первая из них:

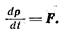
Подставив выражение для р, придем к основ-

ному уравнению релятивистской динамики материальной точки:

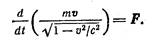
Из сказанного ясно, что в релятивистском случае

масса утрачивает смысл коэффициента пропорциональности между ускорением и силой.

В отличие от ньютоновской механики сила F в релятивистской механике не является инвариантной

(в разных инерциальных системах отсчета она имеет различные модули и направления). Кроме того, ускорение а и сила F оказываются неколлинеарными (направление ускорения, как правило, не совпадает с направлением силы).

Чтобы получить релятивистское выражение для

кинетической энергии, будем исходить из того, что

работа, совершенная над телом, равна приращению

его кинетической энергии:

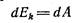
Умножим правую часть равенства E на перемещение частицы ds, а левую часть — на равное ds произведение vdt(ds = vdt). В результате получим соотношение

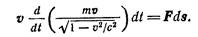
Справа стоит элементарная работа dA. Следователь-

но, левая часть равенства представляет собой прира-

щение кинетической энергии частицы;

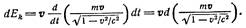
Преобразуем это выражение, воспользовавшись правилом дифференцирования произведения функции

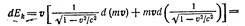
Приведем полученное выражение к общему знамена-

телю и учтем, что v² = v², a vdv = vdv В результате получим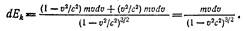

Легко проверить дифференцированием, что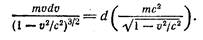

Следовательно

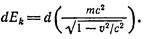
Функции, дифференциалы которых равны друг другу, могут отличаться только на постоянную величину. Поэтому

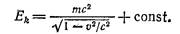
Кинетическая энергия должна обращаться в нуль

вместе со скоростью частицы v. Отсюда следует, что

константа должна быть равна —mс² и соответственно

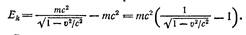
Разложим выражение в ряд со степенями υ / с

При (υ/с)<˂ 1 остальными членами ряда можно пре-

небречь. В результате получится ньютоновское выра-

жение для кинетической энергии: Ек = mv²/2. Это

согласуется с тем, что при скоростях много меньших

скорости света формулы релятивистской механики

должны переходить в соответствующие формулы ньютоновской механики.

Мы уже отмечали, что законы сохранения должны

быть инвариантными по отношению к преобразованиям Лоренца. Как показывает опыт, в частности огромный экспериментальный материал, накопленный в физике элементарных частиц, закон сохранения энергии оказывается инвариантным только в том случае, если свободной (т. е. не подверженной действию сил) частице приписывать, кроме кинетической энергии, дополнительную энергию, равную mс². Таким образом, свободная частица обладает энергией

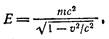которую называют полной энергией.

Неподвижная частица обладает энергией которая называется энергией покоя. Она представляет собой внутреннюю энергию частицы. В случае сложного тела энергия покоя включает в себя, помимо энергий покоя образующих тело частиц, также кинетическую энергию частиц (обусловленную их движением относительно центра масс тела) и энергию их взаимодействия друг с другом. В энергию покоя, как и в полную энергию, не входит потенциальная энергия тела во внешнем силовом поле (Термин «полная энергия» имеет в релятивистской механике иной смысл, чем в ньютоновской механике. В ньютоновской механике полной энергией называется сумма кинетической и потенциальной энергий частицы. В релятивистской механике под полной энергией подразумевается сумма кинетической энергии и энергии покоя частицы.)

Импульс и полная энергия частицы связаны соотношением

Найдем выражение для полной энергии через импульс частицы. Для этого исключим из выражения

для модуля импульса

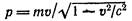и выражения для полной энергии скорость v. В результате получим

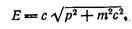
Из этого равенства следует, что

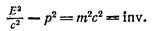
Скорость с и масса m являются инвариантами. Следовательно, и выражение Е2/с2 — р2 п'редставляет cобой инвариант, т. е, имеет одинаковое числовое значение во всех инерциальных системах отсчета. При переходе от одной системы отсчета к другой полная энергия и импульс изменяются, однако числовое значение остается одним и тем же.