Выделим в среде, в которой распространяется плоская продольная волна, элементарный объем ΔV, настолько малый, чтобы деформации и скорости движения во всех точках этого объема можно было считать одинаковыми и равными, соответственно,
Согласно формуле выделенный нами объем будет обладать потенциальной энергией упругой деформации
Где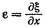 
-относительное удлинение, а Е — модуль Юнга.
Заменим модуль Юнга Е через рv2 (р — плотность среды, v — фазовая скорость волны). Тогда выражение для потенциальной энергии объема ΔV примет вид
(1)
Рассматриваемый объем будет также обладать кинетической энергией
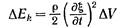(2)
Выражения 1 и 2 в сумме дают полную энергию
Разделив энергию ΔЕ на объем ΔV, в котором она содержится, получим плотность энергии
(3)
Дифференцирование уравнения плоской волны
по t и х дает:
Подставив эти выражения в формулу (3), получим:
(4)
Как следует из (4), плотность энергии в каждый момент времени в разных точках пространства различна.
В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. Поскольку среднее значение квадрата синуса равно половине, среднее (по времени) значение плотности энергии в каждой точке среды будет равно
Плотность энергии и ее среднее значение пропорциональны плотности среды р, квадрату частоты ω и квадрату амплитуды волны а. Подобная зависимость имеет место не только для плоской волны с постоянной амплитудой, но и для других видов волн.
Среда, в которой возникает волна', обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной, следовательно, волна переносит с собой энергию. Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии Ф через поверхность. Поток энергии— скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т. е. совпадает с размерностью мощности. В соответствии
с этим Ф можно измерять в эрг/сек, ваттах и т. д.
Поток энергии в разных точках среды может обладать различной интенсивностью. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.
Пусть, через площадку ΔS1, перпендикулярную к направлению распространения волны, переносится за время Δt энергия ΔE. Тогда плотность потока энергии j по определению равна
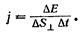
Подставив это выражение для ΔЕ получим
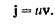
Вектор плотности потока энергии, был впервые введен в рассмотрение выдающимся русским
физиком Н, А, Умовым и называется вектором Умова.
Вектор, как и плотность энергии и, различен в разных точках пространства, а в данной точке пространства изменяется со временем по закону квадрата синуса. Среднее значение его равно
Зная j в некоторой точке пространства, можно найти поток энергии через помещенную в эту точку любым образом ориентированную малую площадку ΔS. Для этого спроектируем ΔS на плоскость, перпендикулярную к вектору j. Величина проекции ΔS1 будет равна
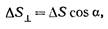
где а — угол, образованный нормалью ɑ к ΔS и вектором j. Вследствие малости ΔS можно считать, что через ΔS течет такой же поток, как и через ΔS1. Поток же через ΔS1 равен
Заменяя ΔS1 его значением, получаем:
Но j׳cosa есть не что иное, как величина составляющей вектора j по направлению нормали п к площадке ΔS:
Следовательно, можно написать, что
Поток энергии через малую площадку ΔS равен произведению нормальной составляющей вектора плотности потока энергии на ΔS.
Зная j в любой точке произвольной поверхности S, можно вычислить поток энергии Ф через эту поверхность. С этой целью разобьем поверхность на элементарные участки ΔS, столь малые, чтобы каждый из них можно было считать плоским, а вектор j в пределах каждого ΔS можно было считать постоянным как по величине, так и по направлению. Тогда элементарный поток ΔФ через каждый участок ΔS можно вычислить по формуле (82.12), беря для каждой ΔS свое значение jn, которое зависит от величины вектора j в том месте, где расположена площадка ΔS, и от ориентации этой площадки по отношению к j.
Полный поток через поверхность S будет равен сумме элементарных потоков:
Полученное нами выражение является приближенным. Чтобы получить точное значение Ф, нужно устремить все ΔS к нулю. При этом сумма перейдет в интеграл
который должен быть взят по всей поверхности S. Формула дает связь между плотностью потока энергии в различных точках поверхности и потоком энергии через эту поверхность.
Вычислим поток энергии через волновую поверхность сферической волны. Нормальная составляющая вектора плотности потока энергии во всех точках волновой поверхности одинакова и имеет среднее значение
(аr — амплитуда волны на расстоянии r от источника).
Вынося постоянное значение jn за знак интеграла, получим:
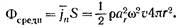
Если энергия волны не поглощается средой, средний поток энергии через сферу любого радиуса должен иметь одинаковое значение:
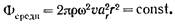
Отсюда следует, что амплитуда а,- сферической волны обратно пропорциональна расстоянию r от источника волны.
Амплитуда плоской волны может быть постоянной лишь при условии, что энергия волны не поглощается средой. В противном случае интенсивность волны с удалением от источника постепенно уменьшается — наблюдается затухание волны. Как показывает опыт, такое затухание происходит по экспоненциальиому закону. Это означает, что амплитуда волны убывает с расстоянием х по закону а = aoe-yx так что уравнение плоской волны имеет вид:
Величина у называется коэффициентом затухания волны (или коэффициентом поглощения волны). Она имеет размерность, обратную размерности длины. Легко сообразить, что величина, обратная y, равна расстоянию, на котором амплитуда волны уменьшается в с раз
Интенсивность волны убывает с расстоянием х по закону
Уравнение сферической волны, распространяющейся в поглощающей среде, имеет вид:
