Релятивистский импульс
Законы сохранения, как и другие законы природы, должны соблюдаться во всех инерциальных системах отсчета, т. е. быть инвариантными по отношению к преобразованиям Лоренца. Проверим, является ли инвариантным закон сохранения импульса, определяемого как произведение массы тела на его скорость: р = mυ.
Рассмотрим абсолютно неупругое центральное соударение двух одинаковых частиц массы т. При указанных на рис. 50.1 условиях суммарный импульc
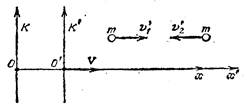
частиц сохраняется в системе К' (до и после соударения он равен нулю), В этой системе компоненты скоростей частиц равньп v'1x́ = V, v'2x́ = — V.
Перейдем в систему К. Согласно формуле
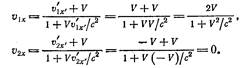
Таким образом, до соударения проекция на ось х суммарного импульса частиц равна
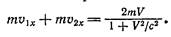
После соударения частицы покоятся в системе К', следовательно, движутся со скоростью V относительно системы К. Поэтому проекция суммарного импульса N равна 2mV.
Полученный нами результат означает, что в системе К закон сохранения импульса, определяемого как mυ, не соблюдается. Только при условии, что скорости частиц много меньше с, отличием выражения от 2mV можно пренебречь. Отсюда следует, что определение импульса в виде mυ пригодно только при условии, что υ˂˂c Для скоростей, сравнимых со скоростью света в вакууме, импульс должен быть определен как-то иначе, причем при v/c→0 это новое выражение для импульса должно переходить в ньютоновское выражение
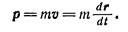
Оказывается, что выражение, обеспечивающее инвариантность закона сохранения импульса, получается из E0.2), если заменить в нем время dt собственным временем частицы dx (которое в отличие от dt является инвариантом). Осуществив такую замену, получим выражение
Здесь dr есть перемещение частицы в той системе отсчета, в которой определяется импульс р, a dτ — промежуток времени, определяемый по часам, движущимся вместе с частицей.
Воспользовавшись формулой D7.3), заменим в
выражении E0.3) промежуток собственного времени dτ промежутком dt, измеренным по часам той системы, в которой определяется импульс частицы (в этой системе частица движется со скоростью v = dr/dt).
В результате получим, что
Таким образом, релятивистское выражение для импульса имеет вид
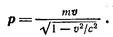
Из формулы E0.4) следует, что зависимость импульса от скорости является более сложной, чем это предполагается в ньютоновской механике При v˂˂с релятивистское выражение для импульса переходит в ньютоновское выражение р = mυ.
Проверим на примере, рассмотренном в начале
этого параграфа, инвариантность закона сохранения импульса, определяемого формулой E0.4). В системе К', очевидно, сумма релятивистских импульсов частиц равна нулю как до, так и после соударения.
В системе К проекция на ось х суммарного импульса частиц до соударения равна
Если считать массу образовавшейся в результате абсолютно неупругого соударения составной частицы равной 2m, то вычисленный по формуле суммарный импульс после соударения окажется равным
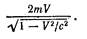
Таким образом, мы пришли к обескураживающему результату: в системе К импульс после соударения отличается от импульса до соударения.
Таким образом, мы пришли к обескураживающему
результату: в системе К импульс после соударения отличается от импульса до соударения.
Причина кажущегося несохранения импульса в
системе К заключается в том, что, масса М составной частицы равна не 2m, a 
Соответственно вычисленный по формуле LE0.4) импульс после соударения будет равен
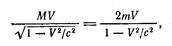
т. е. совпадает с импульсом до соударения.
