Пусть имеются инерциальные системы отсчета К и К'. Безразлично, какую из них считать неподвижной, а какую движущейся.
На рисунке предполагается, что движется система К', в то время как система К неподвижна. С таким же правом можно считать, что неподвижна система К', а система К движется относительно нее со скоростью —V.
Предположим, что происходит какое-то событие. В системе К оно характеризуется значениями координат и времени х, у, z, t; в системе К' — значениями
координат и времени х́ у', z', t'. Найдем формулы, связывающие нештрихованные значения со штрихованными. Из однородности пространства и времени следует, что эти формулы должны быть линейными.
При показанном направлении координатных осей плоскость у' = 0 совпадает с плоскостью y = 0, а плоскость z' = 0 совпадает с плоскостью z = 0. Отсюда вытекает, что, например, координаты у а у' должны обращаться в нуль одновременно, независимо от значений других координат и времени. Это возможно лишь при условии, что 
где вследствие линейности уравнения а — постоянная величина. Ввиду равноправности систем К, и К' обратное преобразование должно иметь вид 
с тем же значением а, что и при прямом преобразовании. Перемножив оба соотношения, найдем, что а2 = 1, откуда а = ±1. Для одинаково направленных осей нужно взять а = +1. В результате находим, что
Аналогичным образом получается формула
Из этих формул вытекает, что значения у и z не зависят от х' и t׳, откуда следует, что значения х' и t' не могут зависеть от у и z׳ соответственно значения х и t не могут зависеть от у' и z'. Это означает, что х и t являются линейными функциями только х' и V.
Точка О имеет координату х = 0 в системе К и х'= —Vt' в системе К'. Следовательно, выражение x'+Vt' должно обращаться в нуль одновременно с координатой х (когда x׳+ Vt' равно нулю, х' =—Vt'). Для этого линейное преобразование должно иметь вид
где у — константа.
Торчка О имеет координату х' = 0 в системе К' и х=Vt в системе K. Следовательно, выражение х - Vt должно обращаться в нуль одновременно с координатой х' (когда х—Vt = 0, то x=Vt). Для этого нужно, чтобы выполнялось соотношение.
где у — константа.
В силу равноправности систем К vt К' коэффициент у в обоих случаях должен быть один и тот же.
Теперь воспользуемся принципом постоянства скорости света. Начнем отсчет времени в обеих системах с того момента, когда начала координат О и О' совпадают. Предположим, что в момент t = t' = 0 в направлении осей х и х' посылается световой сигнал, который производит вспышку света на экране. Это
событие (вспышка) характеризуется в системе К координатой х и временем t, а в системе К' — координатой х' и временем t', причем
(скорость с в обоих случаях одна и та же). Подставив эти значения х и х', получим соотношения
Перемножив эти соотношения и сократив обе части получившегося равенства на tt', придем к уравнению
Отсюда
Где
Подстановка найденного значения у приводит к формулам
Чтобы найти формулы преобразования времени, исключим координату х и разрешим получившееся уравнение относительно t. Затем исключим координату х' и разрешим получившееся уравнение относительно t'. В результате придем к формулам
Напишем вместе формулы подразделив их на две группы:
Эти формулы называются преобразованиями
Лоренца. По формулам осуществляется переход от системы К' к системе К. Вследствие равноправности систем преобразования отличаются лишь знаком перед V. Это отличие обусловлено тем, что система К' движется относительно системы К со скоростью V, в то время как система К движется относительно системы К' со скоростью —V׳.
В преобразованиях Лоренца «перемешаны» координаты и время. Например, время t в системе К определяется не только временем t׳ в системе К', но также и координатой х'. В этом проявляется взаимосвязь пространства и времени.
В пределе при с→о преобразования Лоренца переходят в преобразования Галилея. Таким образом, различие в течение времени в разных инерциальных системах отсчета обусловлено существованием предельной скорости распространения взаимодействий.
При скоростях много меньших скорости света (т. е. при υ<С 1) преобразования Лоренца практически не отличаются от преобразований Галилея. Следовательно, преобразования Галилея сохраняют значение для скоростей, малых по сравнению со скоростью света.
При υ>с выражения для х, t, х' и V становятся мнимыми. В этом проявляется то обстоятельство, что движение со скоростями, большими с, невозможно. Невозможна даже система отсчета, движущаяся со скоростью с, потому что при V = с знаменатели формул для х и t обращаются в нуль.
Преобразованиям Лоренца можно придать симметричный вид, если написать их для х и ct, т. е. для величин одинаковой размерности. В этом случае формулы преобразований выглядят следующим образом:
Формулы для х и ct, а также для x׳ и ct' отличаются друг от друга только перестановкой соответствующих переменных.
Сравним длину стержня в инерциальных системах отсчета К и К' (рис. 47.2). Предположим, что стержень, располо- женный вдоль совпадающих осей х и х', покоится в
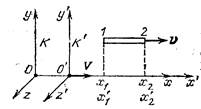
системе К'. Тогда определение его длины в этой си-
стеме не доставляет хлопот. Нужно приложить к
стержню масштабную линейку и определить коорди-
нату х1׳ одного конца стержня, а затем координату
х2׳ другого конца. Разность координат даст длину
стержня l 0 в системе К':
В системе К дело обстоит сложнее. Относительно
этой системы стержень движется со скоростью υ, равной скорости V, с которой система К' движется относительно системы К. Поскольку стержень движется, нужно произвести одновременный отсчет координат его концов x1 и x2 в некоторый момент времени t. Разность координат даст длину стержня l в системе К:
Для сопоставления длин l и l 0 нужно взять ту из
формул преобразований Лоренца, которая связывает
координаты х, х' и время t системы К,. Подстановка в нее значений координат и времени приводит к выражениям
Отсюда
Заменив разности координат длинами стержня, а
относительную скорость V систем К и К' равной ей
скоростью стержня υ, с которой он движется в системе К, придем к формуле
Таким образом, длина движущегося стержня ока-
зывается меньше той, которой обладает стержень в
состоянии покоя. Аналогичный эффект наблюдается
для тел любой формы: в направлении движения линейные размеры тела сокращаются тем больше, чем больше скорость движения. Это явление называется Лоренцевым (или фицджеральдовым) сокращением. Поперечные размеры тела не изменяются. В результате, например, шар принимает форму эллипсоида, сплющенного в направлении движения. Можно показать, что зрительно этот эллипсоид будет восприниматься в виде шара. Это объясняется искажением зрительного восприятия движущихся предметов, вызванным неодинаковостью времен, которые затрачивает свет на прохождение пути от различно удаленных точек предмета до глаза. Искажение зрительного восприятия приводит к тому, что движущийся шар воспринимается глазом как эллипсоид, вытянутый в направлении движения. Оказывается, что изменение формы, обусловленное лоренцевым сокращением, в точности компенсируется искажением зрительного восприятия.
Промежуток времени между событиями. Пусть в
системе К' в одной и той же точке с координатой х'
происходят в моменты времени t'1 и t2 два каких-то
события. Это могут быть, например, рождение элементарной частицы и ее последующий распад. В системе К' эти события разделены промежутком времени
Найдем промежуток времени Δt между событиями в
системе К, относительно которой система К' движет-
ся со скоростью V. Для этого определим в системе К
моменты времени t1 и t2, соответствующие моментам
t1׳ к t'2, и образуем их разность:
' Для сопоставления времен t и t' нужно взять ту из формул преобразований Лоренца, которая связывает t, t' и координату х' системы К'. Подстановка в нее значений координаты и моментов времени приводит к выражениям,
Отсюда
Если события происходят с одной и той же частицей, покоящейся в системе К', то Δt' = t׳2 —t׳1
представляет собой промежуток времени, измеренный по часам, неподвижным относительно частицы и движущимся вместе с ней относительно системы К со скоростью v, равной V. Время, отсчитанное по часам, движущимся вместе с телом, называется собственным временем этого тела и обычно обозначается буквой т. Следовательно, Δt' = Δτ. Величина Δt = t2 —t1 представляет собой промежуток времени между теми же событиями, измеренный по часам системы К, относительно
которой частица (вместе со своими часами) движется со скоростью v. С учетом сказанного формулу можно представить в виде
Из полученной формулы следует, что собственное
время меньше времени, отсчитанного по часам, движущимся относительно тела (очевидно, что часы, неподвижные в системе К, движутся относительно частицы со скоростью —v).
В какой бы системе отсчета не рассматривалось
движение частицы, промежуток собственного времени измеряется по часам системы, в которой частица покоится. Отсюда следует, что промежуток собственного времени является инвариантом, т. е.величиной, имеющей одно и то же значение во всех инерциальных системах отсчета.
С точки зрения наблюдателя, «живущего» в системе К, Δt есть промежуток времени между событиями, измеренный по неподвижным часам, а Δτ —промежуток времени, измеренный по часам, движущимся со скоростью v. Поскольку Δτ < Δt, можно сказать, что движущиеся часы идут
медленнее, чем покоящиеся часы.
В составе космического излучения имеются рождающиеся на высоте 20—30 км нестабильные частицы, называемые мюонами. Они распадаются на электрон (или позитрон) и два нейтрона
Собственное время жизни мюонов (т. е. время жизни, измеренное в системе, в которой они неподвижны) составляет в среднем примерно 2 мкс. Казалось бы, что даже двигаясь со скоростью, очень мало отличающейся от с, они могут пройти лишь путь, равный 600 м. Однако, как показывают измерения, они успевают в значительном количестве достигнуть земной поверхности. Это объясняется тем, что мюоны движутся со скоростью, близкой к с. Поэтому их время жизни, отсчитанное по часам, неподвижным относительно Земли, оказывается значительно большим, чем собственное время жизни этих' частиц Следовательно, не удивительно, что экспериментатор наблюдает пробег мюонов, значительно превышающий 600 м. Для наблюдателя, движущегося вместе с мюонами, расстояние до поверхности Земли сокращается до 600 м поэтому мюоны успевают пролететь расстояние за 2 мкс.
3.Что такое пространство Минковского? Какая физическая величина называется интервалом? Показать что интервал является инвариантом.
Интервал
В обычном пространстве расстояние Δ l между
двумя точками с координатами x1, y1, z1 и х2, y2, z2 определяется выражением
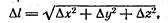
где Δх = х2—x1 и т. д. Это расстояние не зависит от выбора системы координат, т. е. является инвариантом. При переходе к другой координатной системе изменяются величины Δх, Δу и Δz, однако эти изменения таковы, что расстояние Δ l остается одним и тем же.
Казалось бы, что расстояние (или, как принято
говорить, интервал) между двумя мировыми точками в четырехмерном пространстве-времени должно определяться аналогичным выражением
где Δt = t2—t1 и т. д. Однако это выражение непригодно в качестве интервала, поскольку оно не является инвариантом — при переходе к другой инерциальной системе отсчета числовое значение этого выражения изменяется.
Инвариантным является выражение
которое называют интервалом между событиями.
Величина Δs является аналогом расстояния Δ l между, точками в обычном пространстве.
В обычном пространстве справедлива евклидова геометрия, вследствие чего его называют евклидовым. Качественное различие между временем и пространством приводит к тому, что в выражение для интервала квадрат временной координаты и квадраты пространственных координат входят с разными знаками.
Выражение можно написать в виде
где Δ l — расстояние между точками обычного пространства, в которых произошли данные события.
Допустим, что рассматриваются события, происходящие с одной и той же частицей. Тогда отношение Δ l/Δt дает скорость частицы υ. Поэтому, вынеся из-под корня cΔt, получим, что
Выражение Δt 
равно Δτ промежутку собственного времени частицы между событиями. Таким образом, мы приходим к соотoшению
Поскольку с — константа, а Δτ— инвариант, интервал Δs также оказывается инвариантом.
Убедимся в инвариантности интервала еще одним способом. Квадрат интервала в системе К определяется выражением
В системе К' квадрат интервала между теми же событиями равен
Подстановка этих значений дает
(напомним, что β = V/c). Таким образом, инвариантность интервала доказана.
В отличие от расстояния Δ l, квадрат которого
всегда положителен (а само Δ l вещественно), квадрат интервала может быть положительным (если сΔt>Δ l), либо отрицательным (если сΔt<Δ l). либо равным нулю (если сΔt=Δ l). Последний случай имеет место для событий, заключающихся в испускании светового сигнала из одной мировой точки и приходе его в другую, мировую точку (за время Δt световой сигнал проходит в вакууме путь Δ l = cΔ t). Соответственно интервал Δs может быть вещественным (если Δs2>0), мнимым (если Δs2< 0) и равным нулю (для светового сигнала).
Вследствие инвариантности интервал будет вещественным, либо мнимым, либо равным нулю во всех инерциальных системах отсчета.
Для вещественного интервала
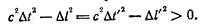
Отсюда следует, что существует такая система К', в которой Δ ĺ =0, т. е. события, разделенные вещественным интервалом, могут быть пространственно совмещенными. Однако не существует системы, в которой Δ t́ ' = 0 (при таком значении Δt' интервал стал бы мнимым). Таким образом, события, разделенные вещественным интервалом, ни в какой системе отсчета не могут быть одновременными. В соответствии с этим вещественные интервалы называются времениподобными.
Для мнимого интервала
Следовательно, существует такая система К', в которой Δ t ' = 0, т. е. события оказываются одновременными. Однако не существует системы, в которой Δ ĺ = 0 (при таком значении Δ l ' интервал стал бы вещественным). Таким образом, события, разделенные мнимым интервалом, ни в какой системе отсчета не могут оказаться пространственно совмещенными,
В соответствии с этим мнимые интервалы называются пространственноподобными.
Расстояние Δt между точками, в которых происходят события, разделенные пространственноподобным интервалом, превышает cΔt. Поэтому такие события
не могут воздействовать друг на друга и, следовательно, не могут быть причинно связанными друг с другом (не существует воздействий, распространяющихся со скоростью, большей с). Причинно связанные события могут быть разделены только времениподобным или нулевым интервалом.
Для события-причины и события-следствия
Согласно последней из формул
Отсюда
Поскольку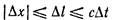 
отношение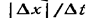 
не превышает с; V<с.
Поэтому, независимо от знака Δх;, правая часть равенства больше нуля и, следовательно, Δt' и Δt имеют одинаковые знаки. Это означает, что событие-причина во всех системах отсчета происходит раньше события-следствия.
