Векторы

1) Трёхмерное пространство

Хорошо известно, что наше пространство трёхмерное, т.е. для обозначения местоположения точки достаточно указать 3 координаты: точки x, y, z.??? координаты удобно обозначать одной и той же буквой, но с различными индексами: 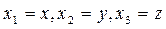. Величины 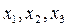являются компонентами радиус-вектора 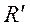,проведенного из начала координат в рассматриваемую точку. Обозначим единичные векторы, нап-равленные вдоль осей 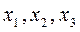через 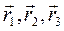. Тогда

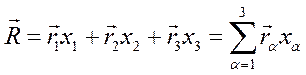(1)

Пусть имеется другая система координат, начало которой сов-падает с рассматриваемой, но оси не совпадают. Для этой системы

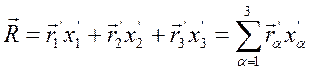(2)

В силу ортогональности система координат имеет соотношение

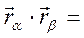0, при 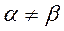; 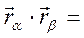1, при 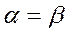(3)

Умножая скалярно обе части (1) на 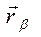, получим с учётом (3) следующее соотношение для компонент :

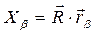(4)

На основании (1) и (2) можно записать

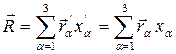(5)

Умножая обе части на 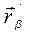и учитывая (3), запишем

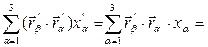{(3):слева не равны 0 толь-

ко компоненты с 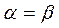,т.е.}= 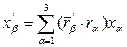(6)

2,2

Введём обозначения для скалярных произведений единичных векторов различных систем координат:

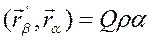(7)

Тогда (6) можно записать

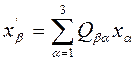(8)

Обратное преобразование получится умножением (5) на 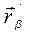. Тогда

.

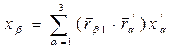Или с учетом (7):

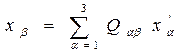
Таким образом, компоненты радиус-вектора преобразуются при переходе от одной СК к другой по формуле (8),т.е.:

,

,

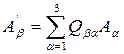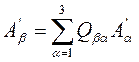То совокупность этих трех величин называются трехмерным вектором, а сами величины 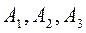называются компонентами вектора по соответствующим осям координат .

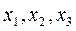Из (1) и (2) с учетом (3) следует:

,

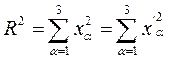Т.е. при преобразованиях сохраняется величина вектора R.

2) Четырехмерный мир

Для полной характеристики события недостаточно указать пространственные координаты этого события, а также указать и время, т.е. событие описывается 4 координатами: x, y, z, t.

Для того, чтобы переход из одной СК в другую описывался (8), удобно в качестве координат использовать:

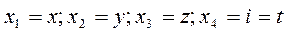
Тогда преобразование Лоренца запишется в виде:

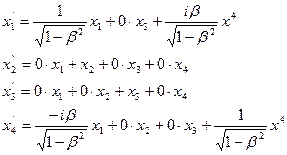
Т.о., это преобразование примет вид:

(9)

Где коэффициенты

 

 

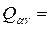
Обратные преобразования аналогично (8) записывают след. образом:

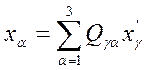
Т.о., в 4-хмерном мире переход от координат мировой точки одной системы отсчета к координатам другой осуществляется с помощью линейных преобразований.