Решение:
1.Определение ускорения точки А.
Так как угловая скорость 
является постоянной, то 
.
Вектор ускорения 
направлен параллельно кривошипу ОА от точки А к точке О.
Выбираем масштаб плана ускорений
Найдём отрезок, изображающий вектор ускорения на плане:
Из полюса плана ускорений 
откладываем данный отрезок в направлении, параллельном АО.
2.Определение ускорения точки В.
Запишем векторное уравнение: 
. Уравнение решаем графически.
Вектор относительного ускорения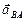 
раскладываем на нормальную и касательную составляющие: 
.
Нормальное относительное ускорение равно:
.
Найдём отрезок, изображающий вектор ускорения 
на плане: 
Продолжаем строить план ускорений, используя правило сложения векторов. Вектор ускорения направлен параллельно АВ. Откладываем отрезок 
из точки 
плана ускорений в указанном направлении от точки В к точке А.
Вектор ускорения 
направлен перпендикулярно АВ. Проводим это направление из точки 
плана ускорений. Вектор ускорения 
направлен параллельно оси x – x. Проводим это направление из полюса . Две прямые линии, проведённые из точек и в указанных направлениях, пересекаются в точке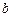 
.
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб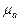 
, получим:
