ЗАДАЧА 1
Выполнить структурный анализ механизма.
Структурная схема механизма.
Звенья механизма
| Звено ззвзвеназвена | Наименование | Подвижность | Число подвижных звеньев |
Кинематические пары
| Обозначение на структурной схеме | Соединяемые звенья | Вид | Тип пары | Индекс пары | |
| Характер соприкосновения | Степень подвижности | ||||
Число одноподвижных кинематических пар p1=7, число двух подвижных кинематических пар р2=0.
Степень подвижности механизма
Строение групп Асcура
А).Последняя группа Асcура
Б).Предпоследняя группа Асcура
В).Начальный механизм
Структурная формула всего механизма
7.Класс всего механизма II, так как наивысший класс группы Ассура, входящей в данный механизм II.
ЗАДАЧА 2
Кинематический расчёт кривошипно-ползунного механизма.
Определение скоростей точек звеньев для заданного положения механизма.
Дано:
Решение
1. Определение скорости точки А.
Вектор скорости 
перпендикулярен кривошипу ОА.
Выбираем масштаб плана скоростей
Найдём отрезок, изображающий вектор скорости 
на плане:
Из полюса плана скоростей 
откладываем данный отрезок в направлении, перпендикулярном ОА в направлении угловой скорости 
.
2. Определение скорости точки В.
Запишем векторное уравнение:
. Уравнение решаем графически.
Направления векторов скоростей: 
, 
.
Продолжим строить план скоростей, используя правило сложения векторов.
Из конца вектора 
(точка 
) проводим направление вектора 
. Из полюса (точка 
) проводим направление вектора 
. На пересечении двух проведённых направлений получим точку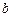 
. Измеряя длины полученных отрезков и умножая их на масштаб 
, получим значения скоростей:
3. Определение скорости точки С.
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
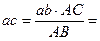мм
Данный отрезок откладываем на продолжении отрезка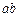 
от точки а. Точку 
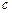соединяем с полюсом .
Величина скорости точки С:
4. Определение угловой скорости шатуна АВ.
с-1
Для определения направления 
переносим вектор в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует . В данном случае угловая скорость направлена ______________________________________________.
| Исследуемая величина | Отрезок на плане | Направление | Величина отрезка на плане, мм | Масштабный коэффициент μv | Значение величины, м/с |
|  
|  
|
| ||
| 
| 
| |||
| 
| 
| |||
| 
| ||||
|
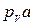
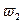
