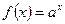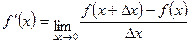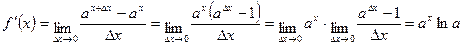Зададим функцию f(x).
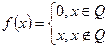Q- множество всех рациональных чисел.
Рациональные числа, как и иррациональные, плотно расположены на числовой оси: то есть между двумя любыми рациональными числами всегда найдется иррациональное и наоборот.
Зададим функцию в окрестности точки x0=0.
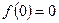(так как 0 рациональное)
Пусть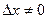 
-любое рациональное число.
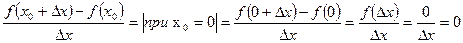
Пусть 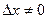- любое иррациональное число.
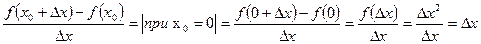
Это означает, что функция f(x) не будет являться непрерывной в окрестности точки 0, посмотрим, будет ли существовать производная в этой точке.
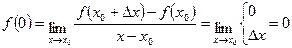
Это означает, что производная в точке x=0 существует.
Значит, функция f(x) разрывна во всех точках, кроме x=0, а значит и в окрестности точки x=0, несмотря на то, что имеет в ней производную.
Таблица производных и свойства производных.
| 
|
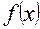
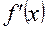
1. 
| 
|
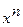
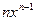
2. 
| 
|
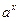
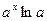
3. 
|
|
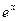
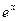
4. 
| 
|
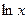
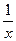
5. 
| 
|
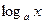
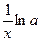
6. 
| 
|
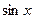
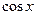
| 7.
| 
|
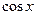
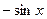
8. 
| 
|
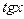
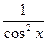
9. 
| 
|
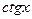
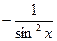
10. 
| 
|
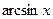
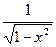
11. 
| 
|
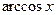
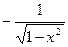
12. 
| 
|
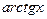
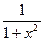
13. 
| 
|
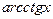
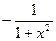
Пример.
