Дифференциальное исчисление функции одной переменной.
Значение функции f(x) в каждой допустимой фиксированной точке x0: f(x0) – число. Изменяя значение аргумента, получаем различные значения функции.
y1=f(x1), y2=f(x2), ……, yn=f(xn).
Возникает вопрос: Как сильно изменится значение функции f(x) при данном изменении аргумента?
Ответ на этот вопрос и приводит к понятию производной.
Пусть задана некоторая функция y=f(x), определенная в окрестности в точке x0.
Определение 1. Если существует конечный предел отношения 
при 
, то его называют производной функции в точке x0.
(*)
где
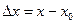- приращение аргумента.
- приращение функции
Определение 2. Если в равенстве (*) даются односторонние пределы, (то есть только левый или только правый), то соответствующие производные называются левой и правой производной.
- левая производная
- правая производная.
Замечание 1. Если левая и правая производные совпадают, то функция имеет производную в этой точке x0.
Замечание 2. Если односторонние производные в точке x0 различны или хотя бы одна из них равна 
, то и производная в этой точке не существует.
