Из существования производной (см.*):
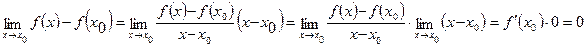
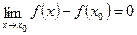
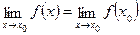
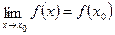
Что и означает, согласно определению 1 параграфа 22, что функция является непрерывной в точке x0.
Замечание 1. Обратное утверждение в общем случае неверно: функция не обязательно имеет производную во всех точках, в которых непрерывна.
Пример1:
Зададим функцию 
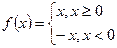
Зададим функцию в точке f(0)=|0|=0 => функция в точке 0 непрерывна.
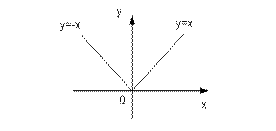
Посмотрим, будет ли она иметь производную в этой точке, для этого вычислим правую и левую производную.
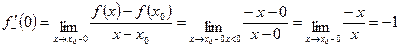
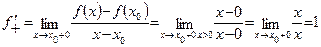
Так как  , то производной в этой точке не существует. Более того, можно построить пример такой функции, которая будет непрерывна во всех точках числовой оси, но не будет иметь производных во всех этих точках. Однако это довольно сложная, объемная процедура.
, то производной в этой точке не существует. Более того, можно построить пример такой функции, которая будет непрерывна во всех точках числовой оси, но не будет иметь производных во всех этих точках. Однако это довольно сложная, объемная процедура.
Замечание 2. Заметим, что теорема 1 гарантирует непрерывность функции, имеющей производную в точке x, только в самой точке x0, но не во всей ее окрестности.






