Колебательный контур — электрическая цепь, содержащая последовательно соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Колебательный контур - простейшая система, в которой могут происходить свободные электромагнитные колебания.
Пусть конденсатор ёмкостью C заряжен до напряжения U0. Энергия, запасённая в конденсаторе составляет
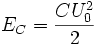
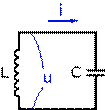
Колебательный контур
При соединении конденсатора с катушкой индуктивности,в цепи потечёт ток I, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия колебательного контура EC = 0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
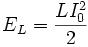, где L — индуктивность катушки, I0 — максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения − U0.
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
В общем, описанные выше процесы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличии от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.
Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.
Чтобы в контуре возникли электрические колебания, его нужно «подтолкнуть»— зарядить конденсатор от какого-либо источника тока, например от батареи, а затем соединить заряженный конденсатор с катушкой индуктивности. С этого момента конденсатор начнет разряжаться через катушку, создавая в колебательном контуре нарастающий электрический ток, а вокруг витков катушки — магнитное поле. Когда конденсатор полностью разрядится, ток через катушку достигнет максимального значения и магнитное поле скажется наиболее сильным — электрический заряд конденсатора преобразовался в магнитное поле катушки. Ток в контуре некоторое время будет идти в том же направлении, но уже за счет убывающей энергии магнитного поля, накопленной катушкой, а конденсатор начнет перезаряжаться. Как только магнитное пате катушки исчезнет, ток в контуре на мгновение прекратится. К этому моменту конденсатор окажется полностью перезаряженным, поэтому через катушку вновь потечет ток, но уже в противоположном направлении. В результате в контуре возникают колебания электрического тока, продолжающиеся до тех вор, пока вся энергия, запасенная конденсатором, не израсходуется на преодоление сопротивления провода катушки индуктивности. Изменяя индуктивность (число витков) катушки и емкость конденсатора, можно в широких пределах изменять частоту колебаний в контуре. Электрические колебания, возбужденные в контуре зарядом конденсатора, свободные, 1 следовательно, затухающие.
Радиотехника очень нуждается в колебаниях электрического тока, которые, возникнув однажды, продолжались бы долгое время. Их легко превратить в непрерывные радиоволны.
Чтобы получить незатухающие колебания, контур, в такт с колебаниями в нем, надо «подталкивать», т. е. пополнять дополнительной энергией. В радиопередатчике колебательный контур получает энергию от высокочастотного генератора, а для приемного контура источником энергии служат электрические колебания высокой частоты, которые возбуждаются радиоволнами в антенне.
Колебательный контур — составная часть радиоприемника. Только благодаря ему удается настроить приемник на частоту той радиовещательной станции, передачу которой мы хотели бы услышать.
Период электромагнитных колебаний в идеальном колебательном контуре (т. е. в таком контуре, где нет потерь энергии) зависит от индуктивности катушки и емкости конденсатора и находится по
формуле Томсона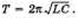 
. Частота с периодом связана обратно пропорциональной зависимостью
В реальном колебательном контуре свободные электромагнитные колебания будут затухающими из-за потерь энергии на нагревание проводов. Для практического применения важно получить незатухающие электромагнитные колебания, а для этого необходимо колебательный контур пополнять электроэнергией, чтобы скомпенсировать потери энергии. Для получения незатухающих электромагнитных колебаний применяют генератор незатухающих колебаний, который является примером автоколебательной системы.
